【题目】某校实行选科走班制度，张毅同学的选择是物理生物政治这三科，且物理在 A 层班级，生物在 B 层班级，该校周一上午课程安排如下表所示，张毅选择三个科目的课各上一节， 另外一节上自习，则他不同的选课方法有（ ）
第一节 | 第二节 | 第三节 | 第四节 |
地理 B 层 2 班 | 化学 A 层 3 班 | 地理 A 层 1 班 | 化学 A 层 4 班 |
生物 A 层 1 班 | 化学 B 层 2 班 | 生物 B 层 2 班 | 历史 B 层 1 班 |
物理 A 层 1 班 | 生物 A 层 3 班 | 物理 A 层 2 班 | 生物 A 层 4 班 |
物理 B 层 2 班 | 生物 B 层 1 班 | 物理 B 层 1 班 | 物理 A 层 4 班 |
政治 1 班 | 物理 A 层 3 班 | 政治 2 班 | 政治 3 班 |
A.8 种B.10 种C.12 种D.14 种
科目：高中数学 来源： 题型：
【题目】经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元.根据历史资料，得到销售季度内市场需求量的频率分布直图，如右图所示.经销商为下一个销售季度购进了130t该农产品.以
（单位：t，100≤≤150)表示下一个销售季度内的市场需求量，T(单位:元)表示下一个销售季度内经销该农产品的利润.
（Ⅰ）将T表示为的函数；
（Ⅱ）根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，
、
是两个小区所在地，、到一条公路
的垂直距离分别为
，
，两端之间的距离为
.
（1）某移动公司将在之间找一点
，在处建造一个信号塔，使得对
、的张角与对
、的张角相等，试确定点的位置.
（2）环保部门将在之间找一点
，在处建造一个垃圾处理厂，使得对、所张角最大，试确定点的位置.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过椭圆
的左顶点
作斜率为2的直线，与椭圆的另一个交点为
，与
轴的交点为
，已知
.
（1）求椭圆的离心率；
（2）设动直线
与椭圆有且只有一个公共点
，且与直线
相交于点
，若
轴上存在一定点
，使得
，求椭圆的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将函数
图象上的所有点的横坐标伸长到原来的2倍，再把所得各点向右平移
个单位长度，最后把所得各点纵坐标扩大到原来的2倍，就得到函数f（x）的图象，则下列说法中正确的个数是（ ）
①函数f（x）的最小正周期为2π；
②函数f（x）的最大值为2；
③函数f（x）图象的对称轴方程为
；
④设x1，x2为方程
的两个不相等的根，则
的最小值为
.
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a R， a0，函数 f (x) eax1 ax ，其中常数e 
.
（1）求 f (x) 的最小值；
（2）当a ≥1时，求证:对任意 x0 ，都有 xf (x) ≥ 2ln x 1 ax2.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥P—ABC中，PB
平面ABC，ABBC，AB=PB=2，BC=2
，E、G分别为PC、PA的中点.
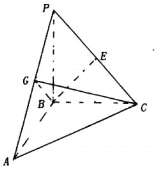
（1）求证：平面BCG平面PAC；
（2）假设在线段AC上存在一点N，使PNBE，求
的值；
（3）在（2）的条件下，求直线
与平面
所成角的正弦值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据中国生态环境部公布的2017年、2018年长江流域水质情况监测数据，得到如下饼图：
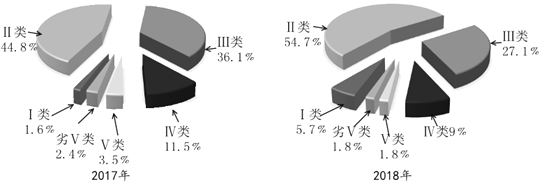
则下列说法错误的是（ ）
A.2018年的水质情况好于2017年的水质情况
B.2018年与2017年相比较，Ⅰ、Ⅱ类水质的占比明显增加
C.2018年与2017年相比较，占比减小幅度最大的是Ⅳ类水质
D.2018年Ⅰ、Ⅱ类水质的占比超过
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某班有甲乙两个物理科代表，从若干次物理考试中，随机抽取八次成绩的茎叶图（其中茎为成绩十位数字，叶为成绩的个位数字）如下：
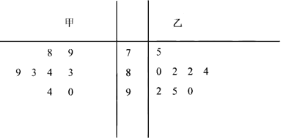
（1）分别求甲、乙两个科代表成绩的中位数；
（2）分别求甲、乙两个科代表成绩的平均数，并说明哪个科代表的成绩更稳定；
（3）将频率视为概率，对乙科代表今后三次考试的成绩进行预测，记这三次成绩中不低于90分的次数为
，求的分布列及均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
