
分析 (1)$\overrightarrow{PH}$=(-1,-y′),$\overrightarrow{PQ}$=(x′,-y′),利用PH⊥PM,求动点M的轨迹E的方程;
(2)联立直线l1:x=my+$\frac{1}{8}$与曲线E,得${y}^{2}-\frac{m}{2}y-\frac{1}{16}=0$,结合韦达定理,即可用m表示四边形ABCD的面积.
解答 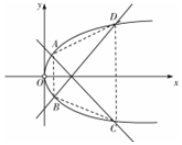 解:(1)设M(x,y),P(0,y′)(y′≠0),Q(x′,0),
解:(1)设M(x,y),P(0,y′)(y′≠0),Q(x′,0),
$\overrightarrow{PH}$=(-1,-y′),$\overrightarrow{PQ}$=(x′,-y′),
∵PH⊥PM,
∴-x′+y′2=0,
∵$x′=\frac{x}{2},y′=-y$,
∴${y}^{2}=\frac{x}{2}$(y≠0);
(2)联立直线l1:x=my+$\frac{1}{8}$与曲线E,得${y}^{2}-\frac{m}{2}y-\frac{1}{16}=0$,
∴yA+yC=$\frac{m}{2}$,yAyC=-$\frac{1}{16}$,
由题意,四边形ABCD是等腰梯形,
∴S=$|\frac{(2{y}_{A}+2{y}_{D})({x}_{D}-{x}_{A})}{2}|$=|$-m({y}_{A}-{y}_{C})^{2}$|=|$\frac{{m}^{2}+m}{4}$|.
点评 本题考查轨迹方程,考查直线与抛物线的位置关系,考查面积的计算,属于中档题.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α=$\frac{π}{4}$,β=-$\frac{π}{4}$ | B. | $α=\frac{2π}{3},β=\frac{π}{6}$ | C. | $α=\frac{π}{3},β=\frac{π}{6}$ | D. | $α=\frac{5π}{6},β=\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
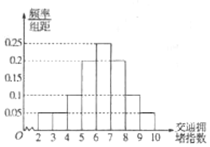 交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2]畅通;T∈[2,4]基本畅通;T∈[4,6]轻度拥堵;T∈[6,8]中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交能指挥中心选取了市区20个交能路段,依据其交能拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6],[6,8],[8,10]的路段中共抽取6个中段,则中度拥堵的路段应抽取3个.
交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2]畅通;T∈[2,4]基本畅通;T∈[4,6]轻度拥堵;T∈[6,8]中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交能指挥中心选取了市区20个交能路段,依据其交能拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6],[6,8],[8,10]的路段中共抽取6个中段,则中度拥堵的路段应抽取3个.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 6 | m | -4 | -6 | -6 | -4 | n | 6 |
| A. | (-3,-1)和(-1,1) | B. | (-3,-1)和(2,4) | C. | (-1,1)和(1,2) | D. | (-∞,-3)和(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{i}{2}$ | B. | -$\frac{i}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
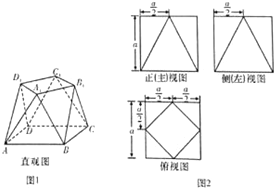 一个多面体的直观图如图1所示,其正(主)视图,侧(左)视图,俯视图如图2所示.
一个多面体的直观图如图1所示,其正(主)视图,侧(左)视图,俯视图如图2所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com