
【题目】某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20,30) | 30 | 18 |
[30,40) | 36 | 24 |
[40,50) | 12 | 9 |
[50,60] | 4 | 3 |
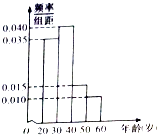
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
【答案】
(1)解:由频率分布直方图知,0.35×40=14
(2)解:由频率分布直方图得:
全校教师的平均年龄为:
25×0.35+35×0.4+45×0.15+55×0.1=35
(3)解:∵在年龄段[20,30)内的教师人数为120×0.35=42(人),从该年龄段任取1人,
由表知,此人A项培训结业考试成绩优秀的概率为 ![]() ,
,
B项培训结业考试成绩优秀的概率为 ![]() ,
,
∴此人A、B两项培训结业考试成绩都优秀的概率为 ![]() ,
,
∵在年龄段[30,40)内的教师人数为120×0.4=48(人),
从该年龄段任取1人,由表知,此人A项培训结业考试成绩优秀的概率为 ![]() ,
,
B项培训结业考试成绩优秀的概率为 ![]() ,
,
∴此人A、B两项培训结业考试成绩都优秀的概率为 ![]()
由题设知X的可能取值为0,1,2.
∴ ![]() ,
,
![]() ,
,
∴X的概率分布为
X | 0 | 1 | 2 |
P |
|
|
|
X的数学期望为 ![]()
【解析】(1)由频率分布直方图能求出从年龄段[20,30)抽取的人数.(2)由频率分布直方图能求出全校教师的平均年龄.(3)由题设知X的可能取值为0,1,2.分别求出相应的概率,由此能求出X的概率分布列和数学期望.
【考点精析】掌握频率分布直方图和离散型随机变量及其分布列是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明一家订阅的晚报会在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(![]() )能否出现
)能否出现![]() 的情况?说明理由.
的情况?说明理由.
(![]() )证明过
)证明过![]() ,
,![]() ,
,![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长为定值.
轴上截得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且S2=11,S5=50,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量的坐标可以是( )
A.(﹣1,﹣3)
B.(1,﹣3)
C.(1,1)
D.(1,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1,y1)∈M,存在(x2,y2)∈M,使x1x2+y1y2=0成立,则称集合M具有∟性,给出下列四个集合:
①M={(x,y)|y=x3﹣2x2+3}; ②M={(x,y)|y=log2(2﹣x)};
③M={(x,y)|y=2﹣2x}; ④M={(x,y)|y=1﹣sinx};
其中具有∟性的集合的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍. 
(1)求椭圆C的方程;
(2)如图,直线l:y=kx+m与椭圆C相交于P,Q两点,若在椭圆C上存在点R,使OPRQ为平行四边形,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com