
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� �ɻ����¼��ĸ����жϣ�1��������˵����2������д��ȫ������ķ��жϣ�3����
��� �⣺��1���¼�C=��������Ʒ��ȫ�Ǵ�Ʒ����������һ����Ʒ��������Ʒ������ȫ����Ʒ�����¼���B?C����B��C�����⣬��1������
��2����a=1��b=0ʱ����$\sqrt{a}$��$\sqrt{b}$��ʱlnb�����壬�ʣ�2������
��3��������p��?x�ʣ�0��$\frac{��}{2}$����x-sinx��0����Vp��?x�ʣ�0��$\frac{��}{2}$����x-sinx��0���ʣ�3����ȷ��
����ȷ��˵��ֻ�У�3����
��ѡ��B��
���� ���⿼�����������ж���Ӧ�ã����黥���¼��ĸ�������ֱ�Ҫ�������ж�������ע��ȫ������ķĸ�ʽ���ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{5}}{5}$ | B�� | $\frac{\sqrt{10}}{5}$ | C�� | $\frac{2\sqrt{5}}{5}$ | D�� | $\frac{2\sqrt{10}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | -2 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x��2����x2-3x+2��0 | B�� | ��x2-3x+2=0����x=2 | ||
| C�� | ��x2-3x+2��0����x��2 | D�� | ��x=2����x2-3x+2��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{1}{2}$��+�ޣ� | B�� | [-$\frac{3}{2}$��+�ޣ� | C�� | [-1��+�ޣ� | D�� | [-2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $-\frac{1}{3}$ | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{16}$ | B�� | $\frac{5}{16}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
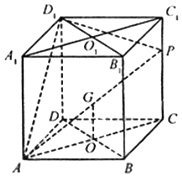 ��ͼ�����ⳤΪ1���������У�P�Dz���CC1�ϵ�һ�㣬CP=m
��ͼ�����ⳤΪ1���������У�P�Dz���CC1�ϵ�һ�㣬CP=m�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com