
分析 (1)将圆C的极坐标方程转化成普通方程,进而转化成圆的标准方程,即可求得圆心C的直角坐标;
(2)将直线l的参数方程代入圆的方程,求得关于t的一元二次方程,令A,B对应参数分别为t1,t2,根据韦达定理t1+t2=-(4+2$\sqrt{3}$)<0,t1•t2=4>0,根据直线与圆的位置关系,即可求得|PA|+|PB|的值.
解答 解:(1)∵ρ=8cosθ,
∴ρ2=8ρcosθ
圆C的直角坐标方程为x2+y2=8x,
∴(x-4)2+y2=16,圆心C为(4,0)┅┅┅┅4分
(2)将直线l的参数方程直线l的参数方程是$\left\{\begin{array}{l}x=-\frac{1}{2}t\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}\right.$,代入x2+y2-8x=0,
得(-$\frac{1}{2}$t)2+(2+$\frac{\sqrt{3}}{2}$t)2-8(-$\frac{1}{2}$t)=0,即t2+(4+2$\sqrt{3}$)t+4=0,┅┅┅┅8分
令A,B对应参数分别为t1,t2,则t1+t2=-(4+2$\sqrt{3}$)<0,t1•t2=4>0,
所以|PA|+|PB|=|t1|+|t2|=|t1+t2|=4+2$\sqrt{3}$┅┅┅┅10分.
点评 本题考查圆的极坐标方程与普通方程得转换,直线与圆的位置关系,考查分析问题及解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 0.9 | 1.9 | 3.2 | 4.4 |
| A. | 0.6 | B. | 0.7 | C. | 0.8 | D. | 0.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
已知函数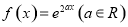 的图像
的图像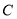 在点
在点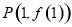 处切线的斜率为
处切线的斜率为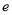 ,记奇函数
,记奇函数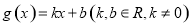 的图像为
的图像为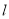 .
.
(1)求实数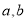 的值;
的值;
(2)当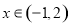 时,图像
时,图像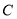 恒在
恒在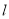 的上方,求实数
的上方,求实数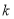 的取值范围;
的取值范围;
(3)若图像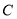 与
与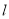 有两个不同的交点
有两个不同的交点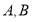 ,其横坐标分别是
,其横坐标分别是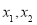 ,设
,设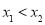 ,求证:
,求证: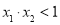 .[来
.[来
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com