
【题目】以下四个命题中正确的是( )
A.空间的任何一个向量都可用其他三个向量表示
B.若![]() 为空间向量的一组基底,则
为空间向量的一组基底,则![]() 构成空间向量的另一组基底
构成空间向量的另一组基底
C.![]() 为直角三角形的充要条件是
为直角三角形的充要条件是![]()
D.任何三个不共线的向量都可构成空间向量的一个基底
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线 (
(![]() 为参数),
为参数),![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(I)写出曲线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(II)在极坐标系中,已知射线![]() 分别与曲线
分别与曲线![]() 及圆
及圆![]() 相交于
相交于![]() ,当
,当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点![]() (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点 |
D.若往容器内再注入 |
其中真命题的代号是: (写出所有真命题的代号).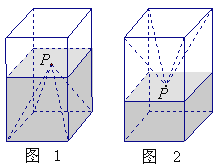
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上一点,
为抛物线上一点,![]() 为坐标原点,
为坐标原点,![]() 的外接圆与抛物线的准线相切,且外接圆的周长为
的外接圆与抛物线的准线相切,且外接圆的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,设不垂直于
,设不垂直于![]() 轴的直线
轴的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若
,若![]() ,证明直线
,证明直线![]() 过定点并写出定点坐标.
过定点并写出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面定义一个同学数学成绩优秀的标志为:“连续![]() 次考试成绩均不低于
次考试成绩均不低于![]() 分”.现有甲、乙、丙三位同学连续
分”.现有甲、乙、丙三位同学连续![]() 次数学考试成绩的记录数据(记录数据都是正整数):
次数学考试成绩的记录数据(记录数据都是正整数):
①甲同学:![]() 个数据的中位数为
个数据的中位数为![]() ,众数为
,众数为![]() ;
;
②乙同学:![]() 个数据的中位数为
个数据的中位数为![]() ,总体均值为
,总体均值为![]() ;
;
③丙同学:![]() 个数据的中位数为
个数据的中位数为![]() ,总体均值为
,总体均值为![]() ,总体方差为
,总体方差为![]() ;
;
则可以判定数学成绩优秀同学为()
A. 甲、丙B. 乙、丙C. 甲、乙D. 甲、乙、丙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的一次真假游戏的有奖竞猜中,设置了“科技”和“生活”这两类试题,规定每位职工最多竞猜3次,每次竞猜的结果相互独立.猜中一道“科技”类试题得4分,猜中一道“生活”类试题得2分,两类试题猜不中的都得0分.将职工得分逐次累加并用X表示,如果X的值不低于4分就认为通过游戏的竞猜,立即停止竞猜,否则继续竞猜,直到竞猜完3次为止.竞猜的方案有以下两种:方案1:先猜一道“科技”类试题,然后再连猜两道“生活”类试题;
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com