练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．设{an}是公比为q的等比数列，则“q＞1”是“{an}为单调递增数列”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 根据等比数列的性质，结合充分条件和必要条件的定义进行判断即可得到结论．

    解答 解：等比数列-1，-2，-4，…，满足公比q=2＞1，但{an}不是递增数列，充分性不成立．
    若an=-1•（$\frac{1}{2}$）n-1为递增数列，但q=$\frac{1}{2}$＞1不成立，即必要性不成立，
    故“q＞1”是“{an}为递增数列”的既不充分也不必要条件，
    故选：D．

    点评 本题主要考查充分条件和必要条件的判断，利用等比数列的性质，利用特殊值法是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．函数f（x）=xlnx的单调递减区间为（　　）
    A．$（0，\frac{1}{e}）$B．$（-∞，\frac{1}{e}）$C．（-∞，-e）D．$（\frac{1}{e}，+∞）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

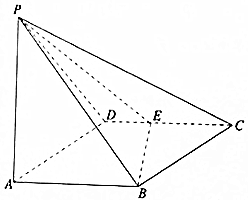    3．如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=2．
    （Ⅰ）证明：平面PBE⊥平面PAB；
    （Ⅱ）求二面角B-PE-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知等差数列{an}的公差d大于0，且a2，a5是方程x2-12x+27=0的两根，数列{bn}的前n项和为Sn，且Sn=$\frac{3}{2}$（bn-1），（n∈N+）．
    （1）求数列{an}，{bn}的通项公式；
    （2）若cn=an•bn，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若幂函数f（x）的图象经过点（2，$\frac{1}{4}$），则f（3）=$\frac{1}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数$f（x）={log_2}（{x^2}+2）$，$\overrightarrow a=（m，1）$，$\overrightarrow b=（\frac{1}{2}，\frac{m}{2}）$，且m＞0，若$f（\overrightarrow a•\overrightarrow b）≥f（|\overrightarrow a-\overrightarrow b|）$，试求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知x，y∈R，满足x2+2xy+4y2=6，则z=x+y的取值范围为$[-\sqrt{6}，\sqrt{6}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知直线l经过点（0，-2），其倾斜角的大小是60°，则直线l与两坐标轴围成三角形的面积S等于（　　）
    A．$\frac{{\sqrt{3}}}{3}$B．$\frac{{2\sqrt{3}}}{3}$C．$\frac{{3\sqrt{3}}}{3}$D．$\frac{{2\sqrt{3}}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．如图，一竖立在地面上的圆锥形物体的母线长为4，一只小虫从圆锥的底面圆上的点P出发，绕圆锥爬行一周后回到点P处，若该小虫爬行的最短路程为$4\sqrt{3}$，则这个圆锥的体积为（　　）
    A．$\frac{{\sqrt{15}}}{3}$B．$\frac{{32\sqrt{35}π}}{27}$C．$\frac{{128\sqrt{2}π}}{81}$D．$\frac{{8\sqrt{3}}}{3}$

    查看答案和解析>>

    同步练习册答案