
【题目】△ABC中,若cos(2B+C)+2sinAsinB=0,则△ABC中一定是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰三角形
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
:![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
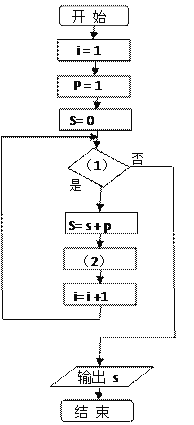
【题目】给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.将右边给出的程序框图补充完整,
(1)___________________ (2)_______________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(
=( ![]() sinx,sinx),x∈R设函数f(x)=
sinx,sinx),x∈R设函数f(x)= ![]() ﹣
﹣ ![]()
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲制作容积为16米3 , 高为1米的无盖长方体容器,已知该容器的底面造价是每平方米1000元,侧面造价是每平方米500元,记该容器底面一边的长为x米,容器的总造价为y元.
(1)试用x表示y;
(2)求y的最小值及此时该容器的底面边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com