
【题目】从1,2,3,4,…,30这30个自然数中任选1个数,求下列事件的概率:
(1)取出的数为偶数;
(2)取出的数能被3整除;
(3)取出的数能被5整除;
(4)取出的数大于8;
(5)取出的数大于8或是偶数;
(6)取出的数能被3或5整除;
(7)取出的数是能被3整除的偶数;
(8)取出的数是偶数或能被5整除.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)![]() (6)
(6)![]() (7)
(7)![]() (8)
(8)![]()
【解析】试题分析:利用古典概型加法公式计算概率.
试题解析:
基本事件空间中含30个基本事件.
(1)事件A=“取出的数为偶数”中含15个基本事件,∴P(A)=![]() .
.
(2)由1≤3x≤30得![]() ≤x≤10,x∈N+,事件B=“取出的数能被3整除”中含10个基本事件,
≤x≤10,x∈N+,事件B=“取出的数能被3整除”中含10个基本事件,
∴P(B)=![]() .
.
(3)由1≤5x≤30得![]() ≤x≤6,∵x∈N+,
≤x≤6,∵x∈N+,
∴事件C=“取出的数能被5整除”中含6个基本事件,∴P(C)=![]() .
.
(4)事件D=“取出的数大于8”中含22个基本事件,∴P(D)=![]() .
.
(5)(方法一)由8<2x≤30,得4<x≤15,
∴P(D∩A)=![]() ,
,
∴事件E=“取出的数大于8或是偶数”的概率
P(E)=P(D∪A)=P(D)+P(A)-P(D∩A)=![]() .
.
(方法二)大于8的数有22个,小于9的偶数有4个,∴事件E含26个基本事件,
∴P(E)=![]() .
.
(6)既能被3整除,又能被5整除的数能被15整除,1到30中能被15整除的数有2个,
∴P(B∩C)=![]() .
.
∴事件F=“取出的数能被3或5整除”的概率为
P(F)=P(B∪C)=P(B)+P(C)-P(B∩C)=![]() .
.
(7)能被3整除的偶数即能被6整除的数,
由1≤6x≤30,得![]() ≤x≤5,
≤x≤5,
∵x∈N+,
∴其概率为P=![]() .
.
(8)取出的数既是偶数又能被5整除时,一定能被10整除,∴有10,20,30,共3个.
∴P(A∩C)=![]() .
.
∴事件G=“取出的数是偶数或能被5整除”的概率P(G)=P(A∪C)=P(A)+P(C)-P(A∩C)=![]() .
.


科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程和相关系数r,分别得到以下四个结论:
① ![]() ②
② ![]()
③ ![]() ④
④ ![]()
其中,一定不正确的结论序号是( )
A.②③
B.①④
C.①②③
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(-1,2)且与两坐标轴的正半轴所围成的三角形面积等于![]() .
.
(1)求直线l的方程.
(2)求圆心在直线l上且经过点M(2,1),N(4,-1)的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
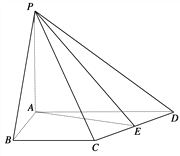
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() .计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
.计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,某公司的32名职工的月工资(单位:元)如下:
职务 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 管理 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5 500 | 5 000 | 3 500 | 3 000 | 2 500 | 2 000 | 1 500 |
(1)求该公司职工工资的平均数、中位数、众数.(精确到1元)
(2)假设副董事长的工资从5 000元提升到20 000元,董事长的工资从5 500元提升到30 000元,那么新的平均数、中位数、众数分别是多少?(精确到1元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如表.
组号 | 年龄 | 访谈人数 | 愿意使用 |
1 | [18,28) | 4 | 4 |
2 | [28,38) | 9 | 9 |
3 | [38,48) | 16 | 15 |
4 | [48,58) | 15 | 12 |
5 | [58,68) | 6 | 2 |
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | |||
不愿意使用的人数 | |||
合计 |
参考公式: ![]() ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com