
 ,等比数列{an}的前n项和为f(n)-c,正项数列{bn}的首项为c,且前n项和Sn满足Sn-Sn-1=
,等比数列{an}的前n项和为f(n)-c,正项数列{bn}的首项为c,且前n项和Sn满足Sn-Sn-1=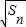 +
+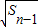 (n≥2).
(n≥2).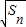 }是等差数列,并求Sn;
}是等差数列,并求Sn; }前n项和为Tn,问
}前n项和为Tn,问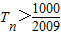 的最小正整数n是多少?
的最小正整数n是多少?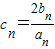 ,求数列{cn}的前n项和Pn.
,求数列{cn}的前n项和Pn. ,
,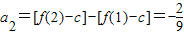 ,
,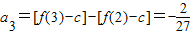 .数列{an}成等比数列,能求出数列{an}的通项公式.
.数列{an}成等比数列,能求出数列{an}的通项公式.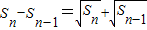 ,n≥2,知
,n≥2,知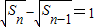 ,(n≥2),由此能够证明数列{
,(n≥2),由此能够证明数列{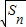 }是等差数列,并求出Sn.
}是等差数列,并求出Sn.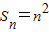 ,当n≥2时,bn=Sn-Sn-1=n2-(n-1)2=2n-1,故
,当n≥2时,bn=Sn-Sn-1=n2-(n-1)2=2n-1,故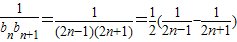 ,由此利用裂项求和法能求出满足
,由此利用裂项求和法能求出满足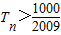 的最小正整数.
的最小正整数.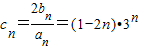 ,知
,知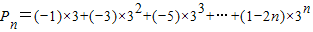 ,由此利用错位相减法能够求出数列{cn}的前n项和Pn.
,由此利用错位相减法能够求出数列{cn}的前n项和Pn. ,
,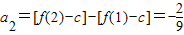 ,
,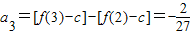 .
.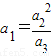 =
=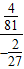 =-
=- =
=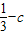 ,
,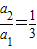 ,
,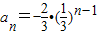 =-2•(
=-2•( )n-1,n∈N*.…(3分)
)n-1,n∈N*.…(3分)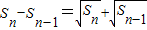 ,n≥2,
,n≥2,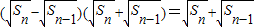 ,n≥2
,n≥2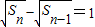 ,(n≥2)…(5分)
,(n≥2)…(5分)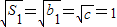
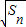 }构成一个首项为1,公差为1的等差数列,
}构成一个首项为1,公差为1的等差数列,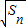 =1+(n-1)×1=n,∴
=1+(n-1)×1=n,∴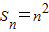 .…(6分)
.…(6分)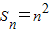 ,
,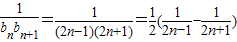 ,
,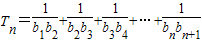
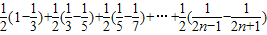
 (1-
(1- )=
)=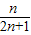 ,…(10分)
,…(10分)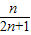 >
>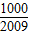 ,得n>
,得n>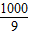 ,
, 的最小正整数为112.…(11分)
的最小正整数为112.…(11分)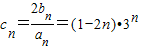 .…(12分)
.…(12分)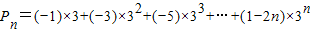 ①
①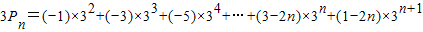 ②
②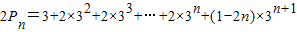
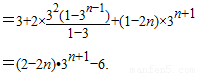
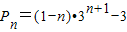 .…(14分)
.…(14分)

科目:高中数学 来源: 题型:
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
 |
| i=1 |
| 2Sn |
| an |
| (n+anbn)2+7-2n |
| n |
| m |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)已知函数![]() ,等比数列{an}的前n项和为f(n)-c.正项数列{bn}的首项为c,且前n项和Sn满足
,等比数列{an}的前n项和为f(n)-c.正项数列{bn}的首项为c,且前n项和Sn满足![]() .
.
⑴ 求c,并求数列{an}和{bn}的通项公式;
⑵ 求数列![]() 的前n项和为Tn;
的前n项和为Tn;
注意:解答请写在答题卷上21题对应位置
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都七中高一(下)期中数学试卷(解析版) 题型:填空题
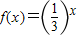 ,等比数列{an}的前n项和为Sn=f(n)-c,则an的最小值为 .
,等比数列{an}的前n项和为Sn=f(n)-c,则an的最小值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com