
【题目】函数f(x)=(x2﹣3)ex , 当m在R上变化时,设关于x的方程f2(x)﹣mf(x)﹣ ![]() =0的不同实数解的个数为n,则n的所有可能的值为( )
=0的不同实数解的个数为n,则n的所有可能的值为( )
A.3
B.1或3
C.3或5
D.1或3或5
【答案】A
【解析】解:函数f(x)=(x2﹣3)ex的导数为f′(x)=(x+3)(x﹣1)ex , 当x>1或x<﹣3时,f′(x)>0,f(x)递增;
当﹣3<x<1时,f′(x)<0,f(x)递减.
即有f(x)在x=1处取得极小值﹣2e;在x=﹣3处取得极大值6e﹣3 ,
作出f(x)的图象,如图所示;
关于x的方程f2(x)﹣mf(x)﹣ ![]() =0,
=0,
由判别式为m2+ ![]() >0,方程有两个不等实根,
>0,方程有两个不等实根,
令t=f(x),则t2﹣mt﹣ ![]() =0,t1t2=﹣
=0,t1t2=﹣ ![]() <0,
<0,
则原方程有一正一负实根.
当t>6e﹣3 , y=t和y=f(x)有一个交点,
当0<t<6e﹣3 , y=t和y=f(x)有三个交点,
当﹣2e<t<0时,y=t和y=f(x)有两个交点,
当t<﹣2e时,y=t和y=f(x)没有交点,
则x的方程f2(x)﹣mf(x)﹣ ![]() =0的实根个数为3.
=0的实根个数为3.
故选:A.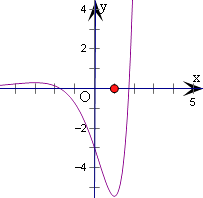


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,棱长为a,E是棱DD1的中点 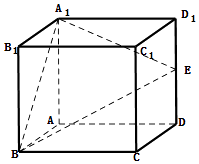
(1)求三棱锥E﹣A1B1B的体积;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有10个著名景点,其中8 个为日游景点,2个为夜游景点.某旅行团要从这10个景点中选5个作为二日游的旅游地.行程安排为第一天上午、下午、晚上各一个景点,第二天上午、下午各一个景点.
(1)甲、乙两个日游景点至少选1个的不同排法有多少种?
(2)甲、乙两日游景点在同一天游玩的不同排法有多少种?
(3)甲、乙两日游景点不同时被选,共有多少种不同排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
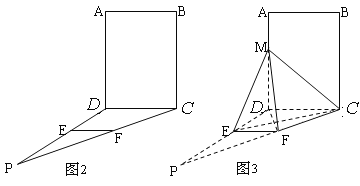
【题目】如图2,四边形![]() 为矩形,
为矩形, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,作如图3折叠,折痕
,作如图3折叠,折痕![]()
![]()
![]() ,其中点
,其中点![]() 分别在线段
分别在线段![]() 上,沿
上,沿![]() 折叠后点
折叠后点![]() 叠在线段
叠在线段![]() 上的点记为
上的点记为![]() ,并且
,并且![]() ⊥
⊥![]() .(1)证明:
.(1)证明: ![]() ⊥平面
⊥平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经济学中,函数f(x)的边际函数M(x)定义为M(x)=f(x+1)﹣f(x),利润函数p(x)边际利润函数定义为M1(x)=p(x+1)﹣p(x),某公司最多生产 100 台报系统装置,生产x台的收入函数为R(x)=3000x﹣20x2(单位:元),其成本函数为C(x)=500x+4000x(单位:元),利润是收入与成本之差.
(1)求利润函数p(x)及边际利润函数M1(x);
(2)利润函数p(x)与边际利润函数M1(x)是否具有相等的最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 任作一条直线与椭圆
任作一条直线与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,试问在
两点,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com