
【题目】和平面解析几何的观点相同,在空间中,空间平面和曲面可以看作是适合某种条件的动点的轨迹,在空间直角坐标系![]() 中,空间平面和曲面的方程是一个三原方程
中,空间平面和曲面的方程是一个三原方程![]() .
.
(1)类比平面解析几何中直线的方程,写出①过点![]() ,法向量为
,法向量为![]() 的平面的点法式方程;②平面的一般方程;③在
的平面的点法式方程;②平面的一般方程;③在![]() ,
,![]() ,
,![]() 轴上的截距分别为
轴上的截距分别为![]() ,
,![]() ,
,![]() 的平面的截距式方程.(不需要说明理由)
的平面的截距式方程.(不需要说明理由)
(2)设![]() 、
、![]() 为空间中的两个定点,
为空间中的两个定点,![]() ,我们将曲面
,我们将曲面![]() 定义为满足
定义为满足![]() 的动点
的动点![]() 的轨迹,试建立一个适当的空间直角坐标系
的轨迹,试建立一个适当的空间直角坐标系![]() ,求曲面
,求曲面![]() 的方程.
的方程.
(3)对(2)中的曲面![]() ,指出和证明曲面
,指出和证明曲面![]() 的对称性,并画出曲面
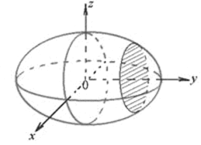
的对称性,并画出曲面![]() 的直观图.
的直观图.
【答案】(1)①![]() ;②
;②![]() ;③
;③![]()
(2)![]()
(3)关于原点对称,关于![]() ,
,![]() ,
,![]() 轴对称,关于
轴对称,关于![]() ,
,![]() ,
,![]() 平面对称,如图
平面对称,如图
【解析】
(1)类比平面中直线的点斜式方程,直线的一般方程,直线的截距式方程即可.
(2)类比平面中的求轨迹方程的方法,设空间中的点![]() ,再根据题意列出方程式化简求解即可.
,再根据题意列出方程式化简求解即可.
(3)根据曲面![]() 方程可判断曲面关于原点对称,关于
方程可判断曲面关于原点对称,关于![]() ,
,![]() ,
,![]() 轴对称,关于
轴对称,关于![]() ,
,![]() ,
,![]() 平面对称再证明画出图像即可.
平面对称再证明画出图像即可.
(1) 类比平面中直线的点斜式方程,直线的一般方程,直线的截距式方程可得:
①![]() ;②
;②![]() ;③
;③![]()
(2) 以两个定点![]() 的中点为坐标原点
的中点为坐标原点![]() ,以
,以![]() 所在的直线为
所在的直线为![]() 轴,以线段
轴,以线段![]() 的垂直平分线为
的垂直平分线为![]() 轴,以与
轴,以与![]() 平面垂直的直线为
平面垂直的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,设
,设![]() ,可得
,可得![]() ,
,![]() .
.
所以![]() .
.
移项得![]()
两边平方,得![]()
∴![]()
两边平方得![]()
即![]() ,两边同除以
,两边同除以![]() ,设
,设![]() 则
则
![]() .
.
因此,可得曲面Γ的方程为![]() .
.
(3)由于点![]() 关于坐标原点
关于坐标原点![]() 的对称点
的对称点![]() 也满足Γ的方程,
也满足Γ的方程,
说明曲面Γ关于坐标原点![]() 对称;
对称;
由于点![]() 关于x轴的对称点
关于x轴的对称点![]() 也满足Γ的方程,
也满足Γ的方程,
说明曲面Γ关于x轴对称;同理,曲面Γ关于y轴对称;关于z轴对称.
由于点![]() 关于
关于![]() 平面的对称点
平面的对称点![]() 也满足Γ的方程,
也满足Γ的方程,
说明曲面Γ关于![]() 平面对称;同理,曲面Γ关于
平面对称;同理,曲面Γ关于![]() 平面对称;关于
平面对称;关于![]() 平面对称.
平面对称.
由以上的讨论,可得曲面Γ的直观图如图所示.



科目:高中数学 来源: 题型:
【题目】在某市高三教学质量检测中,全市共有5000名学生参加了本次考试,其中示范性高中参加考试学生人数为2000人,非示范性高中参加考试学生人数为3000人.现从所有参加考试的学生中随机抽取100人,作检测成绩数据分析.

(1)设计合理的抽样方案(说明抽样方法和样本构成即可);
(2)依据100人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
(3)如果规定成绩不低于130分为特别优秀,现已知语文特别优秀占样本人数的![]() ,语文、数学两科都特别优秀的共有3人,依据以上样本数据,完成列联表,并分析是否有
,语文、数学两科都特别优秀的共有3人,依据以上样本数据,完成列联表,并分析是否有![]() 的把握认为语文特别优秀的同学,数学也特别优秀.
的把握认为语文特别优秀的同学,数学也特别优秀.
语文特别优秀 | 语文不特别优秀 | 合计 | |
数学特别优秀 | |||
数学不特别优秀 | |||
合计 |
参考公式:![]()
参考数据:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 在正方体ABCDA1B1C1D1中,若F,G分别是棱AB,CC1的中点,则直线FG与平面A1ACC1所成角的正弦值等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 的右顶点,点
的右顶点,点![]() 是椭圆
是椭圆![]() 上不同的两点(均异于
上不同的两点(均异于![]() )且满足直线
)且满足直线![]() 与
与![]() 斜率之积为
斜率之积为![]() .试判断直线
.试判断直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由.
是否过定点,若是,求出定点坐标,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:“若![]() ,
,![]() 为异面直线,平面
为异面直线,平面![]() 过直线
过直线![]() 且与直线
且与直线![]() 平行,则直线
平行,则直线![]() 与平面
与平面![]() 的距离等于异面直线
的距离等于异面直线![]() ,
,![]() 之间的距离”为真命题.根据上述命题,若
之间的距离”为真命题.根据上述命题,若![]() ,
,![]() 为异面直线,且它们之间的距离为
为异面直线,且它们之间的距离为![]() ,则空间中与
,则空间中与![]() ,
,![]() 均异面且距离也均为
均异面且距离也均为![]() 的直线
的直线![]() 的条数为( )
的条数为( )
A.0条B.1条C.多于1条,但为有限条D.无数多条
查看答案和解析>>
科目:高中数学 来源: 题型:
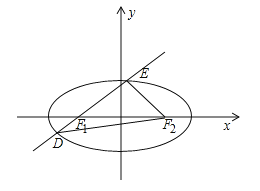
【题目】如图,已知椭圆![]() ,
,![]() 分别为其左、右焦点,过
分别为其左、右焦点,过![]() 的直线与此椭圆相交于
的直线与此椭圆相交于![]() 两点,且
两点,且![]() 的周长为8,椭圆
的周长为8,椭圆![]() 的离心率为
的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在平面直角坐标系![]() 中,已知点
中,已知点![]() 与点
与点![]() ,过
,过![]() 的动直线
的动直线![]() (不与
(不与![]() 轴平行)与椭圆相交于
轴平行)与椭圆相交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点.求证:
轴的对称点.求证:
(i)![]() 三点共线.
三点共线.
(ii)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
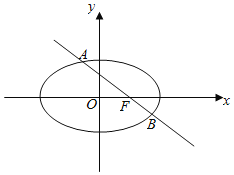
【题目】椭圆C:![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
(1)求椭圆C的方程;
(2)如果直线l的斜率等于-1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用希腊字母![]() 表示,早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第七位的人,这比欧洲早了约1000年,在生活中,我们也可以通过设计下面的实验来估计
表示,早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第七位的人,这比欧洲早了约1000年,在生活中,我们也可以通过设计下面的实验来估计![]() 的值;从区间
的值;从区间![]() 内随机抽取200个数,构成100个数对
内随机抽取200个数,构成100个数对![]() ,其中满足不等式
,其中满足不等式![]() 的数对
的数对![]() 共有11个,则用随机模拟的方法得到的
共有11个,则用随机模拟的方法得到的![]() 的近似值为( )
的近似值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com