
【题目】已知函数f(x)= ![]() x3﹣4x+4,
x3﹣4x+4,
(1)求f(x)的单调区间;
(2)求f(x)在[0,3]上的最大值和最小值.
【答案】
(1)解:因为 ![]() ,所以f'(x)=x2﹣4=(x+2)(x﹣2)…(2分)
,所以f'(x)=x2﹣4=(x+2)(x﹣2)…(2分)
由f'(x)>0得x<﹣2或x>2,
故函数f(x)的单调递增区间为(﹣∞,﹣2),(2,+∞); …
由f'(x)<0得﹣2<x<2
故函数f(x)的单调递减区间为(﹣2,2)
(2)解:令f'(x)=x2﹣4=0得x=±2
由(1)可知,在[0,3]上f(x)有极小值 ![]() ,
,
而f(0)=4,f(3)=1,
因为 ![]()
所以f(x)在[0,3]上的最大值为4,最小值为 ![]() .
.
【解析】(1)求导数,利用导数的正负,即可求f(x)的单调区间;(2)由(1)可知,在[0,3]上f(x)有极小值 ![]() ,而f(0)=4,f(3)=1,即可求f(x)在[0,3]上的最大值和最小值.
,而f(0)=4,f(3)=1,即可求f(x)在[0,3]上的最大值和最小值.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(其中A>0,ω>0,0<φ<
,(其中A>0,ω>0,0<φ<![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M(![]() ,-2).
,-2).
(1)求f(x)的解析式;
(2)将函数f(x)的图象向右平移![]() 个单位后,再将所得图象上各点的横坐标缩小到原来的
个单位后,再将所得图象上各点的横坐标缩小到原来的![]() ,纵坐标不变,得到y=g(x)的图象,求函数y=g(x)的解析式.
,纵坐标不变,得到y=g(x)的图象,求函数y=g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S—ABCD的底面为正方形,SD⊥底面ABCD,则下列结论
①AC⊥SB
②AB∥平面SCD
③SA与平面ABD所成的角等于SC与平面ABD所成的角
④AB与SC所成的角等于DC与SA所成的角.
⑤二面角![]() 的大小为
的大小为![]()
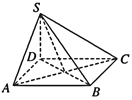
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() ,且
,且![]() 在
在![]() 上单调递增.
上单调递增.
(1)求实数![]() 的值,并写出相应的函数
的值,并写出相应的函数![]() 的解析式;
的解析式;
(2)若![]() 在区间
在区间![]() 上不单调,求实数
上不单调,求实数![]() 的取值范围;
的取值范围;
(3)试判断是否存在正数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() ,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
(1)若a= ![]() ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(2)若f(x)≥g(x)在[1,+∞)上恒成立,求实数a的取值范围;
(3)证明:1+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙俩人各进行3次射击,甲每次击中目标的概率为 ![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ![]() . (Ⅰ)记甲恰好击中目标2次的概率;
. (Ⅰ)记甲恰好击中目标2次的概率;
(Ⅱ)求乙至少击中目标2次的概率;
(Ⅲ)求乙恰好比甲多击中目标2次的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
加工零件x(个) | 10 | 20 | 30 | 40 | 50 |
加工时间y(分钟) | 64 | 69 | 75 | 82 | 90 |
经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数x与加工时间y这两个变量,下列判断正确的是( )
A.成正相关,其回归直线经过点(30,75)
B.成正相关,其回归直线经过点(30,76)
C.成负相关,其回归直线经过点(30,76)
D.成负相关,其回归直线经过点(30,75)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1﹣nan(n∈N*)
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a>0且a≠1.若a=
,其中a>0且a≠1.若a= ![]() 时方程f(x)=b有两个不同的实根,则实数b的取值范围是;若f(x)的值域为[2,+∞),则实数a的取值范围是 .
时方程f(x)=b有两个不同的实根,则实数b的取值范围是;若f(x)的值域为[2,+∞),则实数a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com