
| A. | f(2016)<0 | B. | f(2016)<e${\;}^{-201{6}^{2}}$ | ||
| C. | f(2)<0 | D. | f(2)>e-4032 |
分析 由题意可知f′(x)+2016f(x)>0恒成立,构造函数g(x)=$\frac{f(x)}{{e}^{-2016x}}$,求其导函数,可知其导函数恒大于0,由此可得函数g(x)=$\frac{f(x)}{{e}^{-2016x}}$为实数集上的增函数,由g(2)>g(1)可得f(2)>e-4032.
解答 解:∵f(x)为实数集上的奇函数,且2016f(-x)<f′(x)恒成立,
∴f′(x)+2016f(x)>0恒成立,
令g(x)=$\frac{f(x)}{{e}^{-2016x}}$,
则$g′(x)=\frac{f′(x)•{e}^{-2016x}+2016f(x)•{e}^{-2016x}}{({e}^{-2016x})^{2}}$=$\frac{f′(x)+2016f(x)}{{e}^{-2016x}}>0$,
∴函数g(x)=$\frac{f(x)}{{e}^{-2016x}}$为实数集上的增函数,
又f(1)=e-2016,
∴g(2)>g(1),
即$\frac{f(2)}{({e}^{-2016})^{2}}>\frac{f(1)}{{e}^{-2016}}=\frac{{e}^{-2016}}{{e}^{-2016}}=1$,
∴f(2)>e-4032,
故选:D.
点评 本题考查导数的综合应用,训练了函数构造法,考查了导函数的符号与原函数单调性的关系,是中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
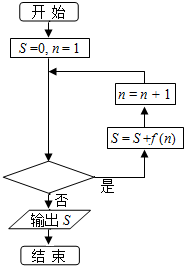 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )| A. | n≤100? | B. | n≤99? | C. | n>100? | D. | n>99? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a,d)∪(b,c) | B. | (c,a]∪[b,d) | C. | (a,c]∪[d,b) | D. | (c,a)∪(d,b) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | -p | D. | (-p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 1条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com