
【题目】《复仇者联盟4:终局之战》是安东尼·罗素和乔·罗素执导的美国科幻电影,改编自美国漫威漫画,自2019年4月24日上映以来票房火爆.某电影院为了解在该影院观看《复仇者联盟4》的观众的年龄构成情况,随机抽取了100名观众的年龄,并分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,得到如图所示的频率分布直方图.
七组,得到如图所示的频率分布直方图.
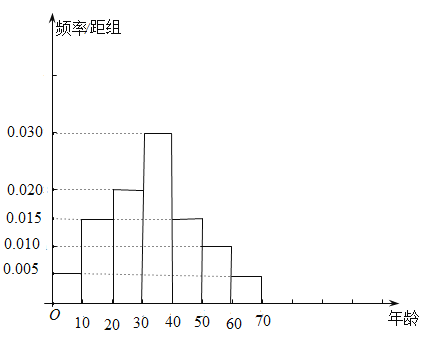
(1)求这100名观众年龄的平均数(同一组数据用该区间的中点值作代表)、中位数;
(2)该电影院拟采用抽奖活动来增加趣味性,观众可以选择是否参与抽奖活动(不参与抽奖活动按原价购票),活动方案如下:每张电影票价格提高10元,同时购买这样电影票的每位观众可获得3次抽奖机会,中奖1次则奖励现金![]() 元,中奖2次则奖励现金
元,中奖2次则奖励现金![]() 元,中奖三次则奖励现金
元,中奖三次则奖励现金![]() 元,其中
元,其中![]() 且
且![]() ,已知观众每次中奖的概率均为
,已知观众每次中奖的概率均为![]() .
.
①以某观众三次抽奖所获得的奖金总额的数学期望为评判依据,若要使抽奖方案对电影院有利,则![]() 最高可定为多少;
最高可定为多少;
②据某时段内的统计,当![]() 时该电影院有600名观众选择参加抽奖活动,并且
时该电影院有600名观众选择参加抽奖活动,并且![]() 每增加1元,则参加抽奖活动的观众增加100人.设该时间段内观影的总人数不变,抽奖活动给电影院带来的利润的期望为
每增加1元,则参加抽奖活动的观众增加100人.设该时间段内观影的总人数不变,抽奖活动给电影院带来的利润的期望为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() 最高定为17元,才能使抽奖方案对电影院有利,②
最高定为17元,才能使抽奖方案对电影院有利,②![]() 时利润
时利润![]() 最大,为
最大,为![]() .
.
【解析】
(1)由频率分布直方图求平均数以及中位数的方法求解即可;
(2)①设观众三次抽奖所获得的奖金总额为随机变量![]() ,
,![]() 可能的取值为0,
可能的取值为0,![]() ,
,![]() ,
,![]() ,求出
,求出![]() 可能取值对应的概率,得出期望,使期望小于等于10,得出对电影院有利时
可能取值对应的概率,得出期望,使期望小于等于10,得出对电影院有利时![]() 的最大值;
的最大值;
②由期望的值以及题设条件得出![]() 的表达式,根据二次函数的性质,得出
的表达式,根据二次函数的性质,得出![]() 的最大值.
的最大值.
(1)平均数![]()
![]()
![]()
![]() ,
,
前三组的频率之和为![]()
前四组为![]()
故中位数落在第4组
设中位数为![]() ,则
,则![]()
解得![]() ,即中位数为
,即中位数为![]() .
.
(2)①设观众三次抽奖所获得的奖金总额为随机变量![]() ,
,![]() 可能的取值为0,
可能的取值为0,![]() ,
,![]() ,
,![]()

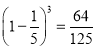
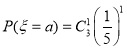
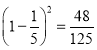
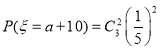
![]()
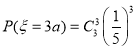
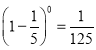
所以,![]()
![]()
令![]() ,解得
,解得![]()
所以![]() 最高定为17元,才能使抽奖方案对电影院有利.
最高定为17元,才能使抽奖方案对电影院有利.
②![]()
![]()
![]()
![]() .
.
![]() 为二次函数,其对称轴
为二次函数,其对称轴![]()
![]() 时,
时,![]() ,
,![]() 时,
时,![]() .
.
![]() ,因此
,因此![]() 时利润
时利润![]() 最大,为
最大,为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】乒乓球赛规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分。设在甲、乙的比赛中,每次发球,甲发球得1分的概率为![]() ,乙发球得1分的概率为
,乙发球得1分的概率为![]() ,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是一个“数阵”:
1 | ( ) | ( ) | ( ) | … |
| … |
( ) | 1 | ( ) | ( ) | … |
| … |
( ) | ( ) | ( ) | 1 | … |
| … |
… | … | … | … | … | … | … |
|
|
|
| … |
| … |
… | … | … | … | … | … | … |
其中每行都是公差不为0等差数列,每列都是等比数列,![]() 表示位于第i行第j列的数.
表示位于第i行第j列的数.
(1)写出![]() 的值:
的值:
(2)写出![]() 的计算公式,以及第2020个1所在“数阵”中所在的位置.
的计算公式,以及第2020个1所在“数阵”中所在的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下说法:
①一年按365天计算,两名学生的生日相同的概率是![]() ;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:an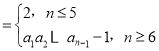 (n∈N*).若正整数k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,则k=( )
(n∈N*).若正整数k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,则k=( )
A.16B.17C.18D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若
,若![]() ,则称数列
,则称数列![]() 为“广义递增数列”,若
为“广义递增数列”,若![]() ,则称数列
,则称数列![]() 为“广义递减数列”,否则称数列
为“广义递减数列”,否则称数列![]() 为“摆动数列”.已知数列
为“摆动数列”.已知数列![]() 共4项,且
共4项,且![]() ,则数列
,则数列![]() 是摆动数列的概率为______.
是摆动数列的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com