
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 且满足
且满足
(1)求角B的大小;
(2)若 的面积为为
的面积为为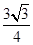 且
且 ,求
,求 的值;
的值;
(1)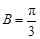 . ⑵a+c=
. ⑵a+c=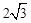 .
.
解析试题分析:(1)又A+B+C=π,即C+B=π-A,
∴sin(C+B)=sin(π-A)=sinA,
将(2a-c)cosB=bcosC,利用正弦定理化简得:(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB=sinCcosB+sinBcosC=sin(C+B)=sinA,
在△ABC中,0<A<π,sinA>0,
∴cosB= ,又0<B<π,则
,又0<B<π,则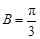 ;
;
(2)∵△ABC的面积为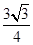 ,sinB=sin
,sinB=sin =
=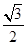 ,
,
∴S= acsinB=
acsinB= ac=
ac=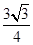 ,
,
∴ac=3,又b=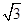 ,cosB=cos
,cosB=cos =
= ,
,
∴由余弦定理b2=a2+c2-2accosB得:a2+c2-ac=(a+c)2-3ac=(a+c)2-9=3,
∴(a+c)2=12,
则a+c=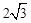 .
.
考点:考查主要考查正弦、余弦定理的应用,诱导公式,两角和与差的正弦函数公式,三角形的面积公式,以及特殊角的三角函数值。
点评:中档题,本题综合考查了正弦、余弦定理的应用,诱导公式,两角和与差的正弦函数公式,三角形的面积公式,以及特殊角的三角函数值。其中(2)将sinB及已知面积代入求出ac的值,利用余弦定理得到b2=a2+c2-2accosB,再利用完全平方公式整理后,按整体思想求出a+c的值。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com