
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,恒有
时,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
附:![]() ,
,![]() .
.
【答案】(1)见解析.(2) ![]() .
.
【解析】
(1)首先求得导函数,然后分类讨论![]() 和
和![]() 两种情况确定函数的单调性即可;
两种情况确定函数的单调性即可;
(2)原问题等价于函数的最大值小于零,结合函数的单调性分类讨论函数的最大值,然后分别求解关于m的不等式即可确定实数![]() 的取值范围.
的取值范围.
(1)![]()
![]()
![]() .
.
①若![]() ,
,![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
②若![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() ;由
;由![]() ,解得
,解得![]() .
.
所以函数![]() 在区间
在区间![]() ,
,![]() 上单调递减;在区间
上单调递减;在区间![]() 上单调递增.
上单调递增.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() ,
,![]() 上单调递减;在区间
上单调递减;在区间![]() 上单调递增.
上单调递增.
(2)由(1)知,![]() .因为
.因为![]() ,所以
,所以![]() .
.
①若![]() ,则
,则![]() ,由
,由![]() ,解得
,解得![]() ;由
;由![]() ,解得
,解得![]() .
.
所以函数![]() 在区间
在区间![]() 上单调递减;在区间
上单调递减;在区间![]() 上单调递增.
上单调递增.
所以当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() ,
,
所以当![]() 时,
时,![]() 恒成立.
恒成立.
②若![]() ,由
,由![]() ,解得
,解得![]() ;由
;由![]() ,解得
,解得![]() 或
或![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递增;在区间
上单调递增;在区间![]() ,
,![]() 上单调递减.
上单调递减.
所以当![]() 时,
时,![]() 取得极小值,极小值为
取得极小值,极小值为![]() ,当
,当![]() 时,
时,![]() 取得极大值,极大值为
取得极大值,极大值为![]() .
.
要使当![]() 时,
时,![]() ,则需
,则需 ,解得
,解得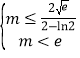 .
.
因为![]()
![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 时,
时,![]() 恒成立.
恒成立.
③若![]() ,由(1)知,函数
,由(1)知,函数![]() 在区间
在区间![]() 上单调递减,又
上单调递减,又![]() ,
,
所以当![]() 时,
时,![]() ,不满足题意.
,不满足题意.
④若![]() ,由(1)知,函数
,由(1)知,函数![]() 在区间
在区间![]() ,
,![]() 上单调递减;在区间
上单调递减;在区间![]() 上单调递增.故当
上单调递增.故当![]() 时,函数
时,函数![]() 取得极小值,极小值为
取得极小值,极小值为![]() ,不满足题意.
,不满足题意.
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积为-2,设点
,且它们的斜率之积为-2,设点![]() 的轨迹是曲线
的轨迹是曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知直线![]() 与曲线
与曲线![]() 相交于不同两点
相交于不同两点![]() 、
、![]() (均不在坐标轴上的点),设曲线
(均不在坐标轴上的点),设曲线![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,若
,若![]() ,垂足为
,垂足为![]() 且
且![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
,![]() ,点P是平面内的动点,且
,点P是平面内的动点,且![]() ,记动点P的轨迹是W.
,记动点P的轨迹是W.
(1)求动点P的轨迹W的方程;
(2)圆![]() 与x轴交于C,D两点,过圆上一动点K(异于C,D点)作两条直线KC,KD分别交轨迹W于G,H,M,N四点.设四边形GMHN面积为S,求
与x轴交于C,D两点,过圆上一动点K(异于C,D点)作两条直线KC,KD分别交轨迹W于G,H,M,N四点.设四边形GMHN面积为S,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,圆
,圆![]() 、椭圆
、椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(Ⅰ)若曲线![]() 与
与![]() 无公共点,求正实数
无公共点,求正实数![]() 的取值范围;
的取值范围;
(Ⅱ)若曲线![]() 的参数方程中,
的参数方程中,![]() ,且曲线
,且曲线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
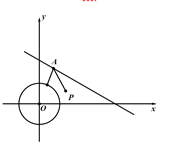
【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马再回到军营,怎样走才能使总路程最短?在如图所示的直角坐标系![]() 中,设军营所在平面区域为
中,设军营所在平面区域为![]() ,河岸线所在直线方程为
,河岸线所在直线方程为![]() .假定将军从点
.假定将军从点![]() 处出发,只要到达军营所在区域即回到军营,则将军可以选择最短路程为_____________.
处出发,只要到达军营所在区域即回到军营,则将军可以选择最短路程为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
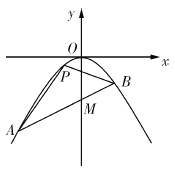
【题目】如图,拋物线的顶点![]() 在坐标原点,焦点在
在坐标原点,焦点在![]() 轴负半轴上,过点
轴负半轴上,过点![]() 作直线
作直线![]() 与拋物线相交于
与拋物线相交于![]() 两点,且满足
两点,且满足![]() .
.
(1)求直线![]() 和拋物线的方程;
和拋物线的方程;
(2)当拋物线上一动点![]() 从点
从点![]() 运动到点
运动到点![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com