
【题目】关于直线![]() 以及平面
以及平面![]() ,下面命题中正确的是( )
,下面命题中正确的是( )
A. 若![]() ,则
,则![]()
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]()
D. 若![]() ,且
,且![]() ,则
,则![]()
【答案】C
【解析】
利用正方体模型,举出A、B、D三项的反例,得出A、B、D三项均为假命题,通过排除法可得C选项为正确答案.
以正方体为例 对于A选项,设下底面ABCD为平面α,在上底面A1D1所在直线为a,B1D1所在直线为b,直线a、b都平行于平面α,但直线a、b不平行,故A项不对 (如图1)

对于B选项,设下底面ABCD为平面α,上底面A1C1所在直线为a,B1D1所在直线为b,直线a是平面α的平行线,直线b与a垂直,但直线b与平面α不垂直,故B选项不对(如图2)
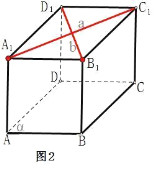
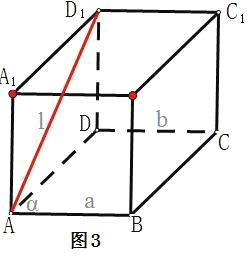
对于D选项,设下底面ABCD为平面α,直线AB、CD所在直线分别为a、b,AD1所在直线为l.可见直线a、b是平面α内的平行线,虽然直线a、b都与直线l垂直,但直线l与平面α不垂直,故D选项不对(如图3)
由A、B、D都不对,得应该选择C选项.
故选:C


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】已知定义在 R 上的奇函数 f (x) ,设其导函数为 f x ,当 x ,0时,恒有xf x f x 0 ,令 F x xf x,则满足 F(3) F 2x 1 的实数 x 的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上, ![]() ⊥
⊥ ![]() ,|
,| ![]() |=|
|=| ![]() |=1,
|=1, ![]() =
= ![]() +
+ ![]() .若|
.若| ![]() |<
|< ![]() ,则|
,则| ![]() |的取值范围是( )
|的取值范围是( )
A.(0, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
奖级 | 摸出红、蓝球个数 | 获奖金额 |
一等奖 | 3红1蓝 | 200元 |
二等奖 | 3红0蓝 | 50元 |
三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额x的分布列与期望E(x).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com