练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某几何体的三视图如图所示，则此几何体的体积为（ ）

    A. B. C. D.

    【答案】C

    【解析】分析: 由三视图还原原几何体，可知该几何体为三棱锥P﹣ABC，底面三角形ABC是等腰直角三角形，然后由棱锥体积公式求解．

    详解: 由三视图还原原几何体如图：

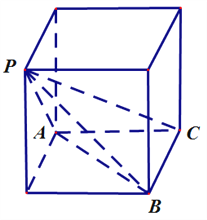
    该几何体为三棱锥P﹣ABC，底面三角形ABC是等腰直角三角形，

    ∴该四面体的体积是V=．

    故选：C．

    点睛: 三视图问题的常见类型及解题策略

    (1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．

    (2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．

    (3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： （）经过点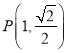，且两焦点与短轴的一个端点的连线构成等腰直角三角形.

    （1）求椭圆的方程；

    （2）动直线： （， ）交椭圆于、两点，试问：在坐标平面上是否存在一个定点，使得以为直径的圆恒过点.若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    当时，讨论函数的单调性；

    求函数在区间上零点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋中装有红球3个、白球2个、黑球1个，从中任取2个，则互斥而不对立的两个事件是　　

    A. 至少有一个白球；都是白球 B. 至少有一个白球；至少有一个红球

    C. 至少有一个白球；红、黑球各一个 D. 恰有一个白球；一个白球一个黑球

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，曲线在点处的切线为．

    （）若直线的斜率为，求函数的单调区间．

    （）若函数是区间上的单调函数，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】汽车的普及给人们的出行带来了诸多方便，但汽车超速行驶也造成了诸多隐患.为了解某一段公路汽车通过时的车速情况，现随机抽测了通过这段公路的200辆汽车的时速，所得数据均在区间中，其频率分布直方图如图所示.

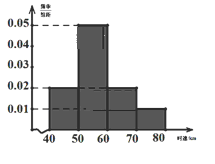
    （1）求被抽测的200辆汽车的平均时速.

    （2）该路段路况良好，但属于事故高发路段，交警部门对此路段过往车辆限速.对于超速行驶，交警部门对超速车辆有相应处罚：记分（扣除驾驶员驾照的分数）和罚款.罚款情况如下：

    超速情况

    10%以内

    10%～20%

    20%～50%

    50%以上

    罚款情况

    0元

    100元

    150元

    可以并处吊销驾照

    ①求被抽测的200辆汽车中超速在10%～20%的车辆数.

    ②该路段车流量比较大，按以前统计该路段每天来往车辆约2000辆.试预估每天的罚款总数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴为极轴建立极坐标系，曲线的极坐标方程为．

    （Ⅰ）求曲线的普通方程和曲线的直角坐标方程；

    （Ⅱ）若曲线和曲线有三个公共点，求以这三个点为顶点的三角形的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】杨辉三角，是二项式系数在三角形中的一种几何排列.在欧洲，这个表叫做帕斯卡三角形，帕斯卡（1623-1662）是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，这是我国数学史上的一个伟大成就.如图所示，在“杨辉三角”中，去除所有为1的项，依次构成数列，则此数列前135项的和为( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在直角坐标系中，曲线C由以原点为圆心，半径为2的半圆和中心在原点，焦点在x轴上的半椭圆构成，以坐标原点为极点，x轴正半轴为极轴建立极坐标系.

    （1）写出曲线C的极坐标方程；

    （2）已知射线与曲线C交于点M，点N为曲线C上的动点，求面积的最大值.

    查看答案和解析>>

    同步练习册答案