
【题目】“大湖名城,创新高地”的合肥,历史文化积淀深厚,民俗和人文景观丰富,科教资源众多,自然风光秀美,成为中小学生“研学游”的理想之地.为了将来更好地推进“研学游”项目,某旅游学校一位实习生,在某旅行社实习期间,把“研学游”项目分为科技体验游、民俗人文游、自然风光游三种类型,并在前几年该旅行社接待的全省高一学生“研学游”学校中,随机抽取了100所学校,统计如下:
研学游类型 | 科技体验游 | 民俗人文游 | 自然风光游 |
学校数 | 40 | 40 | 20 |
该实习生在明年省内有意向组织高一“研学游”学校中,随机抽取了3所学校,并以统计的频率代替学校选择研学游类型的概率(假设每所学校在选择研学游类型时仅选择其中一类,且不受其他学校选择结果的影响):
(1)若这3所学校选择的研学游类型是“科技体验游”和“自然风光游”,求这两种类型都有学校选择的概率;
(2)设这3所学校中选择“科技体验游”学校数为随机变量X,求X的分布列与数学期望.
【答案】(1)![]() (2)分布列见解析,
(2)分布列见解析,![]()
【解析】
(1)统计数据说明学校选择“科技体验游”的概率为![]() ,选择“自然风光游”的概率为
,选择“自然风光游”的概率为![]() ,它们相互独立,两种类型都有学校选择则分为两类:两所学校选“科技体验游”,一所学校选“自然风光游”或者一所学校选“科技体验游”,两所学校选“自然风光游”,由此可计算概率;
,它们相互独立,两种类型都有学校选择则分为两类:两所学校选“科技体验游”,一所学校选“自然风光游”或者一所学校选“科技体验游”,两所学校选“自然风光游”,由此可计算概率;
(2)![]() 可能取值为0,1,2,3.,依次计算出概率可得概率分布列,由期望公式可计算期望.
可能取值为0,1,2,3.,依次计算出概率可得概率分布列,由期望公式可计算期望.
(1)依题意,学校选择“科技体验游”的概率为![]() ,选择“自然风光游”的概率为
,选择“自然风光游”的概率为![]() ,
,
∴若这3所学校选择研学游类型为“科技体验游”和“自然风光游”,则这两种类型都有学校选择的概率为:![]() .
.
(2)![]() 可能取值为0,1,2,3.
可能取值为0,1,2,3.
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.

(1)求图中![]() 的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培驻外方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: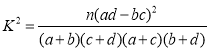 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
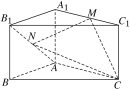
【题目】如图,在直三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=2,点M为A1C1的中点,点N为AB1上一动点.若点N为AB1的中点且CM⊥MN,求二面角MCNA的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著.下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图.下列描述错误的是( )
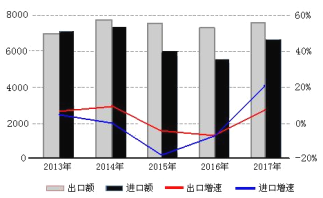
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下列关于函数
,则下列关于函数![]() 的说法,不正确的是( )
的说法,不正确的是( )
A.![]() 的图象关于
的图象关于![]() 对称
对称
B.![]() 在
在![]() 上有2个零点
上有2个零点
C.![]() 在区间
在区间![]() 上单调递减
上单调递减
D.函数![]() 图象向右平移
图象向右平移![]() 个单位,所得图像对应的函数为奇函数
个单位,所得图像对应的函数为奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验中学在教工活动中心举办了一场台球比赛,为了节约时间比赛采取“3局2胜制”.现有甲、乙二人,已知每局甲胜的概率为0.6,乙胜的概率为0.4.求:
(1)这场比赛甲获胜的概率;
(2)这场比赛乙所胜局数的数学期望.
(3)这场比赛在甲获得比赛胜利的条件下,乙有一局获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AC⊥BC,O为AB中点,且DC⊥平面ABC,DC∥BE.已知AC=BC=DC=BE=2.
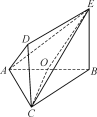
(1)求直线AD与CE所成角;
(2)求二面角O-CE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中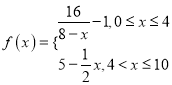 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com