
分析 (1)由$\left\{\begin{array}{l}{m^2}-2m-3=0\\ 2{m^2}+m-1=0\end{array}\right.$,得:m=-1,方程(m2-2m-3)x+(2m2+m-1)y+5-2m=0(m∈R)表示直线,可得m2-2m-3、2m2+m-1不同时为0,即可得出.
(2)方程表示的直线与x轴垂直,可得$\left\{\begin{array}{l}{m^2}-2m-3≠0\\ 2{m^2}+m-1=0\end{array}\right.$,
(3)当5-2m=0,即$m=\frac{5}{2}$时,直线过原点,在两坐标轴上的截距均为0.当$m≠\frac{5}{2}$时,由$\frac{2m-5}{{{m^2}-2m-3}}=\frac{2m-5}{{2{m^2}+m-1}}$,解得:m.
解答 解:(1)由$\left\{\begin{array}{l}{m^2}-2m-3=0\\ 2{m^2}+m-1=0\end{array}\right.$,得:m=-1(12分)
∵方程(m2-2m-3)x+(2m2+m-1)y+5-2m=0(m∈R)表示直线
∴m2-2m-3、2m2+m-1不同时为0,∴m≠-1.(4分)
(2)方程表示的直线与x轴垂直,∴$\left\{\begin{array}{l}{m^2}-2m-3≠0\\ 2{m^2}+m-1=0\end{array}\right.$,∴$m=\frac{1}{2}$.(6分)
(3)当5-2m=0,即$m=\frac{5}{2}$时,直线过原点,在两坐标轴上的截距均为0(8分)
当$m≠\frac{5}{2}$时,由$\frac{2m-5}{{{m^2}-2m-3}}=\frac{2m-5}{{2{m^2}+m-1}}$得:m=-2.(10分)
点评 本题考查了直线方程、相互垂直的直线斜率之间的关系、截距,考查了推理能力与计算能力,属于中档 题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
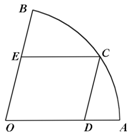 如图,某观光休闲庄园内有一块扇形花卉园OAB,其中O为扇形所在圆的圆心,扇形半径为500米,cos∠AOB=$\frac{1}{4}$.庄园经营者欲在花卉园内修建一条赏花长廊,分别在边OA、弧$\widehat{AB}$、边OB上选点D,C,E修建赏花长廊CD,CE,且CD∥OB,CE∥OA,设CD长为x米,CE长为y米.
如图,某观光休闲庄园内有一块扇形花卉园OAB,其中O为扇形所在圆的圆心,扇形半径为500米,cos∠AOB=$\frac{1}{4}$.庄园经营者欲在花卉园内修建一条赏花长廊,分别在边OA、弧$\widehat{AB}$、边OB上选点D,C,E修建赏花长廊CD,CE,且CD∥OB,CE∥OA,设CD长为x米,CE长为y米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
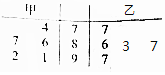 某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.
某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{24}$,0) | B. | ($\frac{5π}{24}$,0) | C. | ($\frac{11π}{24}$,0) | D. | ($\frac{11π}{12}$,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com