
【题目】3月12日,全国政协总工会界别小组会议上,人社部副部长汤涛在回应委员呼声时表示无论是从养老金方面,还是从人力资源的合理配置来说,延迟退休是大势所趋.不过,汤部长也表示,不少职工对于延迟退休有着不同的意见.某高校一社团就是否同意延迟退休的情况随机采访了200名市民,并进行了统计,得到如下的![]() 列联表:
列联表:
赞同延迟退休 | 不赞同延迟退休 | 合计 | |
男性 | 80 | 20 | 100 |
女性 | 60 | 40 | 100 |
合计 | 140 | 60 | 200 |
(1)根据上面的列联表判断能否有![]() 的把握认为对延迟退休的态度与性别有关;
的把握认为对延迟退休的态度与性别有关;
(2)为了进一步征求对延迟退休的意见和建议,从抽取的200位市民中对不赞同的按照分层抽样的方法抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人为男性的概率.
附: 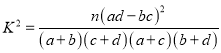 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)根据列联表中的数据求得![]() 后,再结合临界值表中的数据进行判断即可.(2)由题意可得在抽取的不赞同延迟退休的6人中,男性2人,女性4人,然后根据古典概型概率求解可得结论.
后,再结合临界值表中的数据进行判断即可.(2)由题意可得在抽取的不赞同延迟退休的6人中,男性2人,女性4人,然后根据古典概型概率求解可得结论.
试题解析:
(1)由列联表中的数据可得![]() .
.
所以有99.5%的把握认为对延迟退休的态度与性别有关.
(2)设从不赞同延迟退休的男性中抽取![]() 人,从不赞同延迟退休的女性中抽取
人,从不赞同延迟退休的女性中抽取![]() 人,
人,
由分层抽样的定义可知![]() ,解得
,解得![]() ,
,
在抽取的不赞同延迟退休的6人中,男性2人记为![]() ,
, ![]() ,女性4人记为
,女性4人记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则所有的基本事件如下:
,则所有的基本事件如下:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() 共20种,
共20种,
其中至少有1人为男性的情况有16种.
记事件![]() 为“至少有1人为男性不赞同延迟退休”,
为“至少有1人为男性不赞同延迟退休”,
则![]() .
.
即至少有1人为男性不赞同延迟退休的概率为![]() .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |

(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1=1,且an+1-an=n+1(n∈N*),则数列{an}的通项公式为________; ![]() 前10项的和为________.
前10项的和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.在![]() 中,若
中,若![]() ,则
,则![]()
B.在锐角三角形![]() 中,不等式
中,不等式![]() 恒成立
恒成立
C.在![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() 为等腰直角三角形
为等腰直角三角形
D.在![]() 中,若
中,若![]() ,
,![]() ,三角形面积
,三角形面积![]() ,则三角形外接圆半径为
,则三角形外接圆半径为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)经过点(1,
=1(a>b>0)经过点(1,![]() ),且焦距为2
),且焦距为2![]() .
.
(1)求椭圆C方程;
(2)椭圆C的左,右焦点分别为F1,F2,过点F2的直线l与椭圆C交于A,B两点,求△F2AB面积S的最大值并求出相应直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面ADEF,其中四边形ABCD为矩形,四边形ADEF为梯形,AF∥DE,AF⊥EF,AF=AD=2AB=2DE=2.
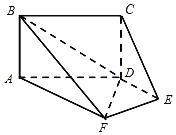
(1)求证:CE∥面ABF;
(2)求直线DE与平面BDF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
【答案】(1) ![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 的极坐标方程为
的极坐标方程为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)先根据三角函数平方关系消参数得曲线![]() ,再根据
,再根据![]() 将曲线
将曲线![]() 的
的![]() 极坐标方程;(2)将
极坐标方程;(2)将![]() 代人曲线
代人曲线![]() 的极坐标方程,再根据
的极坐标方程,再根据![]() 求
求![]() .
.
试题解析:(1)曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)
为参数)
可化为普通方程![]() ,
,
由![]() ,可得曲线
,可得曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径为
的极径为![]() ,
,
射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径满足
的极径满足![]() ,解得
,解得![]() ,
,
所以![]() .
.
【题型】解答题
【结束】
23
【题目】设函数![]() .
.
(1)设![]() 的解集为
的解集为![]() ,求集合
,求集合![]() ;
;
(2)已知![]() 为(1)中集合
为(1)中集合![]() 中的最大整数,且
中的最大整数,且![]() (其中
(其中![]() ,
,![]() ,
,![]() 为正实数),求证:
为正实数),求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com