
【题目】某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为 ![]() ,得到乙公司和丙公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记ξ为该毕业生得到面试的公司个数,若P(ξ=0)=
,得到乙公司和丙公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记ξ为该毕业生得到面试的公司个数,若P(ξ=0)= ![]()
(Ⅰ)求p的值:
(Ⅱ)求随机变量ξ的分布列及数学期望.
【答案】解:(Ⅰ)∵P(ξ=0)= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴p= ![]() .
.
(Ⅱ)ξ的取值为0,1,2,3,
P(ξ=0)= ![]() ;P(ξ=1)=
;P(ξ=1)= ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
P(ξ=2)= ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
P(ξ=3)= ![]() =
= ![]() ,
,
ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
数学期望E(ξ)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]()
【解析】(Ⅰ)利用P(ξ=0)= ![]() ,建立方程,即可求p的值:(Ⅱ)ξ的取值为0,1,2,3,求出相应的概率,即可求随机变量ξ的分布列及数学期望.
,建立方程,即可求p的值:(Ⅱ)ξ的取值为0,1,2,3,求出相应的概率,即可求随机变量ξ的分布列及数学期望.
【考点精析】掌握离散型随机变量及其分布列是解答本题的根本,需要知道在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α< ![]() ),若旋转后的四条线段所围成的封闭图形面积为
),若旋转后的四条线段所围成的封闭图形面积为 ![]() ,则α=( )
,则α=( ) 
A.![]() 或
或 ![]()
B.![]() 或
或 ![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆的一条直径的两个端点分别是(﹣1,3)和(5,﹣5),则此圆的方程是( )
A.x2+y2+4x+2y﹣20=0
B.x2+y2﹣4x﹣2y﹣20=0
C.x2+y2﹣4x+2y+20=0
D.x2+y2﹣4x+2y﹣20=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点. 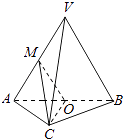
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,∠B的平分线BN所在直线方程为x﹣2y﹣5=0.求:
(1)顶点B的坐标;
(2)直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x| ![]() <2x<4},B={x|0<log2x<2}.
<2x<4},B={x|0<log2x<2}.
(1)求A∩B和A∪B;
(2)记M﹣N={x|x∈M,且xN},求A﹣B与B﹣A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1 , A1D1的中点.
(1)求证:平面CMN∥平面A1DE;
(2)求证:平面A1DE⊥平面A1AE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.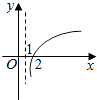
B.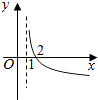
C.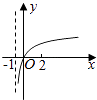
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com