
【题目】若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为( )
A.3
B.2 ![]()
C.2 ![]()
D.3 ![]()
【答案】A
【解析】解:设底面边长AB=a,棱锥的高SM=h, ∵V棱锥S﹣ABCD= ![]() a2h=9,
a2h=9,
∴a2= ![]() ,
,
∵正四棱锥内接于球O,
∴O在直线SM上,设球O半径为R,
(i)若O在线段SM上,如图一,则OM=SM﹣SO=h﹣R,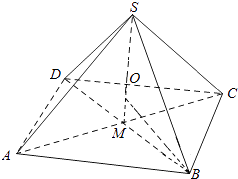
(ii)若O在在线段SM的延长线上,如图二,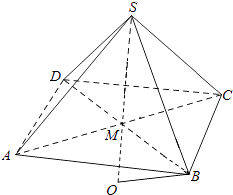
则OM=SO﹣SM=R﹣h,
∵SM⊥平面ABCD,
∴△OMB是直角三角形,
∴OM2+MB2=OB2 ,
∵OB=R,MB= ![]() BD=
BD= ![]() a,
a,
∴(h﹣R)2+ ![]() =R2 , 或(R﹣h)2+
=R2 , 或(R﹣h)2+ ![]() =R2
=R2
∴2hR=h2+ ![]() ,
,
即R= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() ≥3
≥3 ![]() =
= ![]() .
.
当且仅当 ![]() =
= ![]() 取等号,
取等号,
即h=3时R取得最小值 ![]() .
.
故选:A.
【考点精析】关于本题考查的棱锥的结构特征,需要了解侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】设![]() 是正项数列
是正项数列![]() 的前
的前![]() 项和,且
项和,且![]() .
.
(Ⅰ)求数列![]() 通项公式;
通项公式;
(Ⅱ)是否存在等比数列![]() ,使
,使![]() 对一切正整数
对一切正整数![]() 都成立?并证明你的结论.
都成立?并证明你的结论.
(Ⅲ)设![]() (
(![]() ),且数列
),且数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知下列条件解三角形:
①A=60°,a= ![]() ,b=1;
,b=1;
②A=30°,a=1,b=2;
③A=30°,c=10,a=6;
④A=30°,c=10,a=5,
其中有唯一解的序号为( )
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
,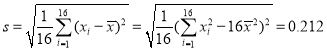 ,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ–3σ<Z<μ+3σ)=0.997 4,0.997 416≈0.959 2,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 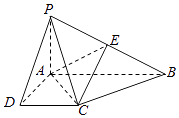
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若对任意的x1 , x2∈[1,a+1],总有|f(x1)﹣f(x2)|≤4,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com