练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数f（x）=2 
    1
    x-3
    的值域是（　　）
    分析：先求指数部分
    1
    x-3
    的范围，再根据指数函数y=2t的单调性求解此函数的值域即可．
    解答：解：令t=
    1
    x-3
    ，则t≠0
    因为y=2t是指数函数，所以0＜2t≠20=1，
    即0＜y且y≠1．
    故选D．
    点评：本题主要考查了利用指数函数的单调性及指数函数的特殊点的函数值求解函数的值域，属于基础试题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2012-2013学年河南省南阳市五校高三（上）期中数学试卷（文科）（解析版） 题型：解答题

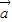    已知向量=（cosωx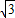，sin（π-ωx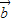）），=（cosωx，sin（+ωx）），（ω＞0），函数f（x）=2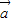•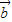+1的最小正周期为2．
    （1）求ω的值；
    （2）求函数f（x）在区间[0，]上的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江西省上饶市广丰中学高三（上）第一次段考数学试卷（文科）（补习班）（解析版） 题型：解答题

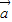    已知向量=（cosωx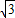，sin（π-ωx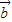）），=（cosωx，sin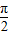（+ωx）），（ω＞0），函数f（x）=2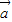•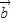+1的最小正周期为2．
    （1）求ω的值；
    （2）求函数f（x）在区间[0，]上的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年安徽省蚌埠一中高三（上）期中数学试卷（文科）（解析版） 题型：解答题

    已知向量=（cosωx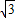，sin（π-ωx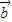）），=（cosωx，sin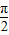（+ωx）），（ω＞0），函数f（x）=2•+1的最小正周期为2．
    （1）求ω的值；
    （2）求函数f（x）在区间[0，]上的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省南平市邵武一中高三（上）期末数学试卷（理科）（解析版） 题型：解答题

    已知向量=（cosx，sinx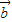），=（-cosx，cosx）
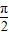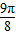    （1）当x∈[，]时，求函数f（x）=2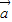•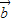+1的最大值．
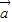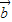    （2）设f（x）=2•+1，将函数y=f（x）的图象向右平移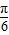个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求y=g（x）的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源：2007年北京市朝阳区高考数学一模试卷（理科）（解析版） 题型：解答题

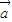    已知向量=（cosx，sinx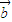），=（-cosx，cosx），函数f（x）=2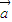•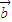+1．
    （Ⅰ）求函数f（x）的最小正周期；
    （Ⅱ）当x∈[0，2π]时，求f（x）的单调减区间．

    查看答案和解析>>

    同步练习册答案