
 ,求此圆锥的体积;
,求此圆锥的体积; ,求∠AOQ的大小.
,求∠AOQ的大小.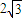 ,我们求出圆锥的底面半径OA长及圆锥的高SO,代入圆锥体积公式,即可得到圆锥的体积;
,我们求出圆锥的底面半径OA长及圆锥的高SO,代入圆锥体积公式,即可得到圆锥的体积;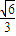 ,设OA=OB=R,∠AOQ=α,进而可求出∠AOQ的大小.
,设OA=OB=R,∠AOQ=α,进而可求出∠AOQ的大小.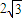
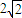
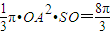 .
.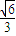 .
.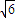 :3.
:3.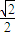 MB=
MB=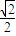 R(1+cosα)
R(1+cosα)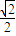 R(1+cosα)=
R(1+cosα)=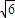 :3.
:3.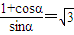
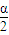 =
=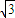


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.
如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.
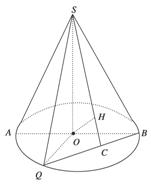
(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2![]() ,求此圆锥的体积.
,求此圆锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.

(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2![]() ,求此圆锥的体积.
,求此圆锥的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com