Question

【题目】已知，两点，满足:，，，则的最大值为________.

Answer 1

【答案】

【解析】

设A（x1，y1），B（x2，y2），＝（x1，y1），＝（x2，y2），由圆的方程和向量数量积的定义、坐标表示，可得三角形OAB为等边三角形，AB＝1，的几何意义为点A，B两点到直线x+y﹣1＝0的距离d1与d2之和，由两平行线的距离可得所求最大值.

解：设A（x1，y1），B（x2，y2），

＝（x1，y1），＝（x2，y2），

由x12+y12＝1，x22+y22＝1，x1x2+y1y2＝，

可得A，B两点在圆x2+y2＝1上，

且＝1×1×cos∠AOB＝，

即有∠AOB＝60°，

即三角形OAB为等边三角形，AB＝1，

的几何意义为点A，B两点

到直线x+y﹣1＝0的距离d1与d2之和，

显然A，B在第三象限，AB所在直线与直线x+y＝1平行，

可设AB：x+y+t＝0，（t＞0），

由圆心O到直线AB的距离d＝，

可得2＝1，解得t＝，

即有两平行线的距离为＝，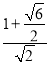

即的最大值为，

故答案为：.