
在 中,
中,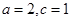 ,则角
,则角 的取值范围是( )
的取值范围是( )
A. | B. | C.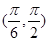 | D. |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:单选题
一艘船上午9:30在A处,测得灯塔S在它的北偏东300处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东750,且与它相距8 海里,则此船的航速是( )
海里,则此船的航速是( )
| A.24海里/小时 | B.30海里/小时 | C.32海里/小时 | D.40海里/小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
| A.直角三角形 | B.锐角三角形 |
| C.钝角三角形 | D.不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为 ( ).
| A.直角三角形 | B.锐角三角形 |
| C.钝角三角形 | D.不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com