
【题目】某码头有总重量为![]() 吨的一批货箱,对于每个货箱重量都不超过
吨的一批货箱,对于每个货箱重量都不超过![]() 吨的任何情况,都要一次运走这批货箱,则至少需要准备载重
吨的任何情况,都要一次运走这批货箱,则至少需要准备载重![]() 吨的卡车( )
吨的卡车( )
A.![]() 辆B.
辆B.![]() 辆C.
辆C.![]() 辆D.
辆D.![]() 辆
辆
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() 。
。![]() 表示集合A中任意两个不同元素的和的不同值的个数。
表示集合A中任意两个不同元素的和的不同值的个数。
(1)若![]() ,分别求
,分别求![]() 和
和![]() 的值;
的值;
(2)若集合![]() ,求
,求![]() 的值,并说明理由;
的值,并说明理由;
(3)集合![]() 中有2019个元素,求
中有2019个元素,求![]() 的最小值,并说明理由。
的最小值,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B两地相距24km.甲车、乙车先后从A地出发匀速驶向B地.甲车从A地到B地需行驶25min;乙车从A地到B地需行驶20min.乙车比甲车晚出发2min.
(1)分别写出甲、乙两车所行路程关于甲车行驶时间的函数关系式;
(2)甲、乙两车何时在途中相遇?相遇时距A地多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 分别是棱
分别是棱![]() 上的点,平面
上的点,平面![]() 平面
平面![]()
(Ⅰ)确定点![]() 的位置,并说明理由;
的位置,并说明理由;
(Ⅱ)求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
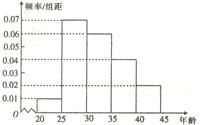
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有200人参加了一次会议,为了了解这200人参加会议的体会,将这200人随机号为001,002,003,…,200,用系统抽样的方法(等距离)抽出20人,若编号为006,036,041,176, 196的5个人中有1个没有抽到,则这个编号是( )
A. 006B. 041C. 176D. 196
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是梯形,AB//DC,
是梯形,AB//DC,![]() ,
,![]()

(1).求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的正弦值
的平面角的正弦值
(3).在线段![]() 上是否存在一点
上是否存在一点![]() ,使AP//平面
,使AP//平面![]() .若存在,请确定点
.若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com