
【题目】已知函数 ![]() .
.
(I) 讨论函数![]() 的单调区间;
的单调区间;
(II)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 上的最大值为3,求
上的最大值为3,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时, ![]() 在
在![]() 内单调递增,
内单调递增, ![]() 在
在![]() 内单调递减;当
内单调递减;当![]() 时,
时, ![]() 在
在![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 在
在![]() 内单调递增,
内单调递增, ![]() 在
在![]() 内单调递减;(Ⅱ)即
内单调递减;(Ⅱ)即![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:
(Ⅰ)对函数求导可得![]() ,令
,令![]() 得
得![]() .
.
分类讨论可得当![]() 时,
时, ![]() 在
在![]() 内单调递增,
内单调递增, ![]() 在
在![]() 内单调递减;当
内单调递减;当![]() 时,
时, ![]() 在
在![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 在
在![]() 内单调递增,
内单调递增, ![]() 在
在![]() 内单调递减;
内单调递减;
(Ⅱ)当![]() 时,函数的解析式
时,函数的解析式![]() ,则
,则![]() ,讨论函数的单调性可得
,讨论函数的单调性可得![]() ,
, ![]() ,且
,且![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(I)![]() .
.
令![]() 得
得![]() .
.
(i)当![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递增.
单调递增.
(ii)当![]() ,即
,即![]() 时,
时,
当![]() 时
时![]() ,
, ![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时
时![]() ,
, ![]() 在
在![]() 内单调递减.
内单调递减.
(iii)当![]() ,即
,即![]() 时,
时,
当![]() 时
时![]() ,
, ![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时
时![]() ,
, ![]() 在
在![]() 内单调递减.
内单调递减.
综上,当![]() 时,
时, ![]() 在
在![]() 内单调递增,
内单调递增, ![]() 在
在![]() 内单调递减;
内单调递减;
当![]() 时,
时, ![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 在
在![]() 内单调递增,
内单调递增,
![]() 在
在![]() 内单调递减.(其中
内单调递减.(其中![]() )
)
(II)当![]() 时,
时, ![]() ,
, ![]()
令![]() ,得
,得![]() .
.
将![]() ,
, ![]() ,
, ![]() 变化情况列表如下:
变化情况列表如下:
|
|
|
| 1 |
|
|
| 0 |
| 0 |
|
| ↗ | 极大 | ↘ | 极小 | ↗ |
由此表可得![]() ,
, ![]() .
.
又![]() ,
,
故区间![]() 内必须含有
内必须含有![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示.
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少? 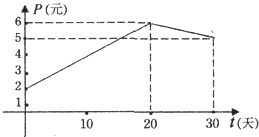
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,h(x)=2f(x)﹣ax﹣b.
,h(x)=2f(x)﹣ax﹣b.
(Ⅰ)判断f(x)的奇偶性,并说明理由;
(Ⅱ)若f(x)为奇函数,且h(x)在[﹣1,1]有零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,Sn为前n天两只老鼠打洞长度之和,则Sn=尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点B是以AC为直径的圆周上的一点,PA=AB=BC,AC=4,PA⊥平面ABC,点E为PB中点. 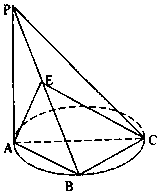
(Ⅰ)求证:平面AEC⊥平面PBC;
(Ⅱ)求直线AE与平面PAC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
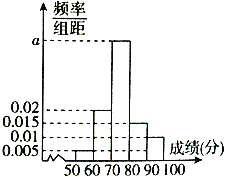
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示.成绩落在[70,80)中的人数为20.
男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(Ⅰ)求a和n的值;
(Ⅱ)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数m;
和中位数m;
(Ⅲ)成绩在80分以上(含80分)为优秀,样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,完成2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=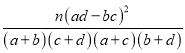 .
.
P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com