
| A. | $\frac{4}{45}$ | B. | -$\frac{4}{45}$ | C. | ±$\frac{4}{45}$ | D. | ±3 |
分析 化简可得x+x-1=(x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$)2-2=7,x2+x-2=(x+x-1)2-2=47,从而解得.
解答 解:∵x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$=3,
∴x+x-1=(x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$)2-2=7,
x2+x-2=(x+x-1)2-2=47,
故$\frac{x+{x}^{-1}-3}{{x}^{2}+{x}^{-2}-2}$=$\frac{7-3}{47-2}$=$\frac{4}{45}$,
故选:A.
点评 本题考查了完全平方式的变形应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2$\sqrt{2}$)∪(2$\sqrt{5}$,+∞) | B. | (2$\sqrt{2}$,3$\sqrt{2}$] | C. | (3$\sqrt{2}$,2$\sqrt{5}$] | D. | [2$\sqrt{2}$,2$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
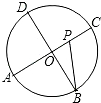 如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )
如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )| A. | 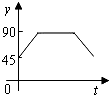 | B. | 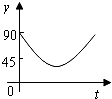 | C. |  | D. | 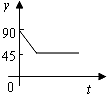 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com