
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 4 |
分析 由正弦定理化简已知等式可得:4sinBsinAcosA=sinAsinB,结合sinA≠0,sinB≠0,可求cosA的值,进而利用余弦定理即可计算得解.
解答 解:∵2bsin2A=asinB,
∴由正弦定理可得:4sinBsinAcosA=sinAsinB,
又∵A,B为三角形内角,sinA≠0,sinB≠0,
∴cosA=$\frac{1}{4}$,
∵b=2,c=3,
∴由余弦定理可得:a=$\sqrt{{b}^{2}+{c}^{2}-2bccosA}$=$\sqrt{4+9-2×2×3×\frac{1}{4}}$=$\sqrt{10}$.
故选:B.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
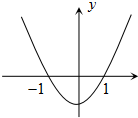 设f(x)=ax3+bx2+cx的极小值为-2,其导函数y=f′(x)的图象是经过点(-1,0),(1,0)开口向上的抛物线,如图所示.
设f(x)=ax3+bx2+cx的极小值为-2,其导函数y=f′(x)的图象是经过点(-1,0),(1,0)开口向上的抛物线,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 因为函数y=sinx(x∈R)的值域为[-1,1],2x-1∈R,所以y=sin(2x-1)(x∈R)的值域也为[-1,1] | |
| B. | 昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿 | |
| C. | 在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c则a∥c,将此结论放到空间中也是如此 | |
| D. | 如果一个人在墙上写字的位置与他的视线平行,那么,墙上字迹离地的高度大约是他的身高,凶手在墙上写字的位置与他的视线平行,福尔摩斯量得墙壁上的字迹距地面六尺多,于是,他得出了凶手身高六尺多的结论 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|x>2} | D. | {x|x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com