【题目】
的内角
的对边分别为
，已知
(1)求
；
(2)若
，求
面积的最大值.
【答案】(1)
；(2)
.
【解析】试题分析：(1)由正弦定理及两角和的正弦公式,三角形内角和公式可得
,进而得；(2)由余弦定理可得
,由基本不等式,得
,代入三角形面积公式,可得三角形面积的最大值.
试题解析： (1)因为
所以由正弦定理得
...........................2分
所以
即
.....................3分
因为
，所以，又
，解得...................5分；
(2)由余弦定理得
，即...................6分
由不等式得
，当且仅当
时，取等号，所以
，
解得...................8分
所以
的面积为
所以面积的最大值为...................10分.
口算题卡加应用题集训系列答案科目：高中数学 来源： 题型：
【题目】某企业生产A，B两种产品，生产1吨A种产品需要煤4吨、电18千瓦；生产1吨B种产品需要煤1吨、电15千瓦。现因条件限制，该企业仅有煤10吨，并且供电局只能供电66千瓦，若生产1吨A种产品的利润为10000元；生产1吨B种产品的利润是5000元，试问该企业如何安排生产，才能获得最大利润？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为了了解一年内的用水情况，抽取了10天的用水量如下表所示：
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量／吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
（Ⅰ）在这10天中，该公司用水量的平均数是多少？每天用水量的中位数是多少？
（Ⅱ）你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量
．
(1)若
分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1,2,3,4,5,6）先后抛掷两次时第一次、第二次出现的点数，求满足
的概率；
(2)若在连续区间
上取值，求满足
的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，圆
的参数方程为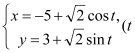
为参数），在以原点
为极点，
轴的非负半轴为极轴建立的极坐标系中，直线
的极坐标方程为
.
（1）求圆
的普通方程和直线
的直角坐标方程；
（2）设直线
与
轴，
轴分别交于
两点，点
是圆
上任一点，求
两点的极坐标和
面积的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4—4：坐标系与参数方程
已知平面直角坐标系
，以
为极点，
轴的非负半轴为极轴建立极坐标系，
点的极坐标为
，曲线
的参数方程为
（
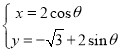为参数）.
（1）写出点
的直角坐标及曲线
的直角坐标方程；
（2）若
为曲线
上的动点，求
中点
到直线
的距离的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了保护环境，2015年合肥市胜利工厂在市政府的大力支持下，进行技术改进：把二氧化碳转化为某种化工产品，经测算，该处理成本
（万元）与处理量
（吨）之间的函数关系可近似地表示为：
且每处理一吨二氧化碳可得价值为20万元的某种化工产品．
（1）当
时，判断该技术改进能否获利？如果能获利，求出最大利润；如果不能获利，则国家至少需要补贴多少万元，该工厂才不亏损？
（2）当处理量为多少吨时，每吨的平均处理成本最少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
