
【题目】如图,已知正方形ABCD的中心为E(﹣1,0),一边AB所在的直线方程为x+3y﹣5=0,求其它三边所在的直线方程. 
【答案】解:E到直线x+3y﹣5=0距离是 ![]() =
= ![]() ,所以E到另三边距离也是
,所以E到另三边距离也是 ![]()
有一条边CD与AB:x+3y﹣5=0平行,设为x+3y+a=0,则 ![]() ,即|a﹣1|=6
,即|a﹣1|=6
∴a=﹣5,a=7 其中a=﹣5就是已知的
∴CD方程为:x+3y+7=0
另两条和他们垂直,所以斜率为3,设为:3x﹣y+b=0
则 ![]() ,即|b﹣3|=6
,即|b﹣3|=6
∴b=9,b=﹣3
∴AD的方程:3x﹣y﹣3=0;BC的方程:3x﹣y+9=0
【解析】先求正方形中心E(﹣1,0)到直线x+3y﹣5=0的距离,然后设出所求直线方程,利用正方形的中心到三边等距离,分别求出所求直线的方程.
【考点精析】认真审题,首先需要了解一般式方程(直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0)).
(A,B不同时为0)).


科目:高中数学 来源: 题型:
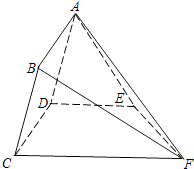
【题目】如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2, ![]() ,CF=6,∠CFE=45°.
,CF=6,∠CFE=45°.
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)在线段CF上求一点G,使锐二面角B﹣EG﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
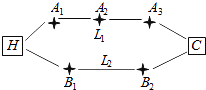
【题目】如图,李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为 ![]() ;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为 ![]() ,
, ![]() .
. 
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点. 
(1)求证:EF∥面PBC
(2)求证:平面PBC⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C与两平行直线 x﹣y﹣8=0和x﹣y+4=0相切,圆心在直线2x+y﹣10=0上.
(1)求圆C的方程.
(2)过原点O做一条直线,交圆C于M,N两点,求OM*ON的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
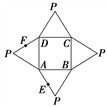
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值;
(3)在棱AD上是否存在一点P,使得BP∥平面AD1E?若存在,求DP的长;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com