
【题目】已知向量 ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),且x∈[﹣
),且x∈[﹣ ![]() ,
, ![]() ]
]
(1)求 ![]()
![]() 及|
及| ![]() +
+ ![]() |;
|;
(2)若f(x)= ![]()
![]() ﹣|
﹣| ![]() +
+ ![]() |,求f(x)的最大值和最小值.
|,求f(x)的最大值和最小值.
【答案】
(1)解:∵ ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),
),
∴ ![]()
![]() =cos
=cos ![]() x cos
x cos ![]() ﹣sin
﹣sin ![]() xsin
xsin ![]() =cos2x.
=cos2x.
| ![]() +
+ ![]() |=|(cos
|=|(cos ![]() x,sin
x,sin ![]() x)+(cos
x)+(cos ![]() ,﹣sin
,﹣sin ![]() )|=|(
)|=|( ![]() )|
)|
= ![]() =
= ![]() =2cosx(x∈[﹣
=2cosx(x∈[﹣ ![]() ,
, ![]() ])
])
(2)解:∵ ![]()
![]() =cos2x,|
=cos2x,| ![]() +
+ ![]() |=2cosx,
|=2cosx,
∴f(x)= ![]()
![]() ﹣|
﹣| ![]() +
+ ![]() |=cos2x﹣2cosx=2cos2x﹣2cosx﹣1.
|=cos2x﹣2cosx=2cos2x﹣2cosx﹣1.
令t=cosx,
∵x∈[﹣ ![]() ,
, ![]() ],∴t∈[
],∴t∈[ ![]() ,1].
,1].
∴y=f(x)= ![]() .
.
∴当t= ![]() ,即x=
,即x= ![]() 时,y有最小值为
时,y有最小值为 ![]() ;
;
当t=1,即x=0时,y有最大值为 ![]() .
.
【解析】(1)由数量积的坐标运算结合两角和的余弦求 ![]()
![]() ;由向量的坐标加法运算求
;由向量的坐标加法运算求 ![]() +
+ ![]() ,然后利用模的公式求模;(2)把(1)中的结果代入f(x)=
,然后利用模的公式求模;(2)把(1)中的结果代入f(x)= ![]()
![]() ﹣|
﹣| ![]() +
+ ![]() |,整理后利用配方法结合x的范围得答案.
|,整理后利用配方法结合x的范围得答案.
【考点精析】通过灵活运用三角函数的最值,掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 即可以解答此题.
即可以解答此题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,cos2B﹣5cos(A+C)=2.
(1)求角B的值;
(2)若cosA= ![]() ,△ABC的面积为10
,△ABC的面积为10 ![]() ,求BC边上的中线长.
,求BC边上的中线长. 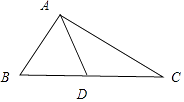
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为![]() ,则称该数为“完美四位数”,如数字“
,则称该数为“完美四位数”,如数字“![]() ”.试问用数字
”.试问用数字![]() 组成的无重复数字且大于
组成的无重复数字且大于![]() 的“完美四位数”有( )个
的“完美四位数”有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个非零向量 ![]() 、
、 ![]() 不共线.
不共线.
(1)若 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3(
=3( ![]() ﹣
﹣ ![]() ),求证:A、B、D三点共线;
),求证:A、B、D三点共线;
(2)求实数k使k ![]() +
+ ![]() 与2
与2 ![]() +k
+k ![]() 共线.
共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com