
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,以
,以![]() 为圆心的圆记为圆
为圆心的圆记为圆![]() ,已知圆
,已知圆![]() 上的点与圆
上的点与圆![]() 上的点之间距离的最大值为21.
上的点之间距离的最大值为21.
(1)求圆![]() 的标准方程;
的标准方程;
(2)求过点![]() 且与圆
且与圆![]() 相切的直线的方程;
相切的直线的方程;
(3)已知直线![]() 与
与![]() 轴不垂直,且与圆
轴不垂直,且与圆![]() ,圆
,圆![]() 都相交,记直线
都相交,记直线![]() 被圆
被圆![]() ,圆
,圆![]() 截得的弦长分别为
截得的弦长分别为![]() ,
,![]() .若
.若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)因为![]() ,可得圆
,可得圆![]() 为圆心,半径为
为圆心,半径为![]() ,设
,设![]() 为圆心的圆记为圆
为圆心的圆记为圆![]() ,设
,设![]() 半径为
半径为![]() ,由圆
,由圆![]() 上的点与圆
上的点与圆![]() 上的点之间距离的最大值为
上的点之间距离的最大值为![]() ,可得
,可得![]() ,即可求得圆
,即可求得圆![]() 方程,即可求得答案;
方程,即可求得答案;
(2)分别讨论切线的斜率不存在和切线的斜率存在两种情况,当切线的斜率存在时,设直线方程为![]() ,设直线到圆的距离为
,设直线到圆的距离为![]() ,由直线和圆相切,可得
,由直线和圆相切,可得![]() ,求得
,求得![]() ,即可求得答案;
,即可求得答案;
(3)设直线![]() 的方程为
的方程为![]() ,求得圆心
,求得圆心![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,
,![]() ,根据几何关系可得:
,根据几何关系可得:![]() ,
,![]() ,结合
,结合![]() ,即可求得
,即可求得![]() 和
和![]() 关系式,即可求得
关系式,即可求得![]() 方程,进而求得直线
方程,进而求得直线![]() 过定点.
过定点.
(1)![]()
![]()
![]() 圆
圆![]() 为圆心,半径为
为圆心,半径为![]()
设![]() 为圆心的圆记为圆
为圆心的圆记为圆![]() ,设
,设![]() 半径为
半径为![]()
由圆![]() 上的点与圆
上的点与圆![]() 上的点之间距离的最大值为
上的点之间距离的最大值为![]() .
.
可得![]()
解得![]()
![]() 圆
圆![]() 的标准方程为
的标准方程为![]() .
.
(2)①当切线的斜率不存在时,直线方程为![]() 符合题意;
符合题意;
②当切线的斜率存在时,
设直线方程为![]() ,
,
即![]() ,
,
![]() 直线和圆相切,
直线和圆相切,
设直线到圆的距离为![]()
![]()
![]() ,
,
解得![]() ,从而切线方程为
,从而切线方程为![]() .
.
故切线方程为![]() 或
或![]()
(3)设直线![]() 的方程为
的方程为![]() ,
,
则圆心![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,
,![]() ,
,
几何关系可得:![]() ,
,![]()
![]()
![]() ,
,![]() .
.
由![]() ,得
,得 ,
,
整理得![]() ,故
,故![]() ,
,
即![]() 或
或![]() ,
,
![]() 直线
直线![]() 为
为![]() 或
或![]() ,
,
![]() 直线
直线![]() 过点定点
过点定点![]() 或直线
或直线![]() 过定点
过定点![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】有编号为1,2,3…n的n个学生,入座编号为1,2,3…n的n个座位,每个学生规定坐一个座位, 设学生所坐的座位号与该生的编号不同的学生人数为![]() , 已知
, 已知![]() 时, 共有6种坐法.
时, 共有6种坐法.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计,得到如下数据:
年龄( |
|
|
|
|
|
患病人数( |
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)计算变量![]() 、
、![]() 的相关系数
的相关系数![]() (计算结果精确到
(计算结果精确到![]() ),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若
),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若![]() ,则
,则![]() 、
、![]() 相关性很强;若
相关性很强;若![]() ,则
,则![]() 、
、![]() 相关性一般;若
相关性一般;若![]() ,则
,则![]() 、
、![]() 相关性较弱.)
相关性较弱.)
参考数据:![]() .
.
参考公式: ,
,
相关系数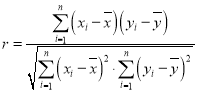 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树林的边界是直线![]() (如图
(如图![]() 所在的直线),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于
所在的直线),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于![]() 的垂线
的垂线![]() 上的点
上的点![]() 点和
点和![]() 点处,
点处,![]() (
(![]() 为正常数),若兔子沿
为正常数),若兔子沿![]() 方向以速度
方向以速度![]() 向树林逃跑,同时狼沿线段
向树林逃跑,同时狼沿线段![]() 方向以速度
方向以速度![]() 进行追击(
进行追击(![]() 为正常数),若狼到达
为正常数),若狼到达![]() 处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
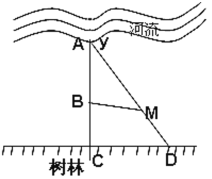
(1)求兔子的所有不幸点(即可能被狼吃掉的点)的区域面积![]() ;
;
(2)若兔子要想不被狼吃掉,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,–2),C(4,1).
(1)若![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量![]() ,
,![]() ,若k
,若k![]() –
–![]() 与
与![]() +3
+3![]() 平行,求实数
平行,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校参加期中考试的高一学生中随机抽取100名得到这100名学生语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() .
.
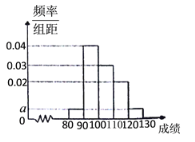
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分,众数,中位数;
(3)已知学生![]() 的语文成绩为123分,现从成绩在
的语文成绩为123分,现从成绩在![]() 中的学生中随机抽取2人参加演讲赛,求学生
中的学生中随机抽取2人参加演讲赛,求学生![]() 被抽中的概率.
被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲箱中装有3个红球,2个黑球,乙箱中装有2个红球,3个黑球,这些球除颜色外完全相同,某商场举行有奖促销活动,规定顾客购物1000元以上,可以参与抽奖一次,设奖规则如下:每次分别从以上两个箱子中各随机摸出2个球,共4个球,若摸出4个球都是红球,则获得一等奖,奖金300元;摸出的球中有3个红球,则获得二等奖,奖金200元;摸出的球中有2个红球,则获得三等奖,奖金100元;其他情况不获奖,每次摸球结束后将球放回原箱中.
(1)求在1次摸奖中,获得二等奖的概率;
(2)若3人各参与摸奖1次,求获奖人数X的数学期望![]() ;
;
(3)若商场同时还举行打9折促销活动,顾客只能在两项促销活动中任选一项参与.假若你购买了价值1200元的商品,那么你选择参与哪一项活动对你有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠APC=90°,∠BPD=120°,PB=PD.
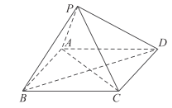
(1)求证:平面APC⊥平面BPD;
(2)若AB=2AP=2,求三棱锥C-PBD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com