练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知（1-2x）n展开式中，奇数项的二项式系数之和为64，则（1-2x）n（1+x）展开式中含x2项的系数为（ ）
    A．71
    B．70
    C．21
    D．49
    【答案】分析：由题意可得 2n=2×64，解得n=7．故（1-2x）n（1+x）=（1-2x）7（1+x） 展开式中含x2项的系数为
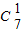
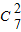
    （-2）•1+•（-2）2，运算求得结果．
    解答：解：已知（1-2x）n展开式中，奇数项的二项式系数之和为64，则2n=2×64，解得n=7．
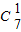
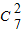
    （1-2x）n（1+x）=（1-2x）7（1+x） 展开式中含x2项的系数为 （-2）•1+•（-2）2=70，
    故选B．
    点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，
    属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知（1-2x）n展开式中，奇数项的二项式系数之和为64，则（1-2x）n（1+x）展开式中含x2项的系数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知（1+2x）n的展开式中，第六项和第七项的二项式系数最大．
    （1）求n的值；
    （2）求展开式中系数最大的项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知（1+2
    		x
    ）n展开式中某项的系数恰为它的前一项系数的2倍，而等于它后一项系数的
    5
    6
    ，求该展开式中二项式系数最大的项．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知（1+2
    		x
    ）n展开式中某项的系数恰为它的前一项系数的2倍，而等于它后一项系数的
    5
    6
    ，求该展开式中二项式系数最大的项．

    查看答案和解析>>

    同步练习册答案