【题目】如图，将长为4，宽为1的长方形折叠成长方体ABCD-A1B1C1D1的四个侧面，记底面上一边
，连接A1B,A1C,A1D.
（1）求长方体ABCD-A1B1C1D1体积的最大值 ；
（2）当长方体ABCD-A1B1C1D1的体积最大时，求二面角B-A1C-D的大小.
【答案】(1)1;(2)
【解析】
（1）用
表示出长方体ABCD-A1B1C1D1体积为：
，
，求该二次函数类型函数的最大值即可。
（2）由（1）得
时，长方体ABCD-A1B1C1D1体积最大，此时该几何体为正方体，过点
作
垂直A1C于点E，连接ED，则
就是二面角B-A1C-D的一个平面角，解三角形
即可。
（1）长方体ABCD-A1B1C1D1体积为：，，当时，
，所以长方体ABCD-A1B1C1D1体积的最大值为1.
（2）由（1）得时，长方体ABCD-A1B1C1D1体积最大，此时该几何体为正方体，过点作垂直A1C于点E，连接ED，
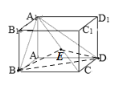
由正方体可得：
,所以就是二面角B-A1C-D的一个平面角，
在正方体ABCD-A1B1C1D1中可得：
，
，
在三角形由余弦定理得：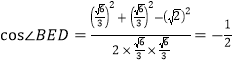
所以
天天向上口算本系列答案科目：高中数学 来源： 题型：
【题目】2018年9月16日下午5时左右，今年第22号台风“山竹”在广东江门川岛镇附近正面登陆，给当地人民造成了巨大的财产损失，某记者调查了当地某小区的100户居民由于台风造成的经济损失，将收集的数据分成
，
，
，
，
五组，并作出如下频率分布直方图.
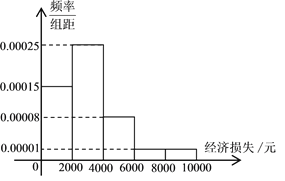
（Ⅰ）根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.
（Ⅱ）“一方有难，八方支援”，台风后居委会号召小区居民为台风重灾区捐款，
记者调查的100户居民捐款情况如下表格，在如图表格空白处填写正确数字，并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
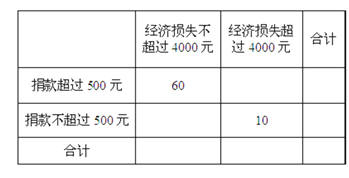
参考公式：
，其中
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，点
在倾斜角为
的直线
上，以坐标原点
为极点，以
轴正半轴为极轴，建立极坐标系，曲线
的方程为
.
（1）写出
的参数方程及
的直角坐标方程；
（2）设
与
相交于
两点，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义在
上的函数
,其导函数
的大致图像如图所示,则下列叙述正确的是().
（1）
（2）函数在
上递增，在
上递减
（3）的极值点为c，e
（4）的极大值为
A. (1)(2) B. (2)(3) C. (3) D. (1)(4)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
是定义在
上的偶函数，且当
时， 
．现已画出函数
在
轴左侧的图象，如图所示，并根据图象：
（1）直接写出函数
， 
的增区间；
（2）写出函数
， 
的解析式；
（3）若函数
， 
，求函数
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知正方体ABCD-A1B1C1D1的棱长为2，E为棱CC1的中点，点M在正方形BCC1B1内运动，且直线AM//平面A1DE,则动点M 的轨迹长度为（ ）
A. 
B. π C. 2 D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
