
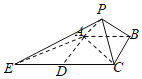
【题目】已知正方形![]() 的边长为2,分别以
的边长为2,分别以![]() ,
,![]() 为一边在空间中作正三角形
为一边在空间中作正三角形![]() ,
,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】2019年11月15日,我市召开全市创建全国文明城市动员大会,会议向全市人民发出动员令,吹响了集结号.为了了解哪些人更关注此活动,某机构随机抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在
.把年龄落在![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为
内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为![]() .
.
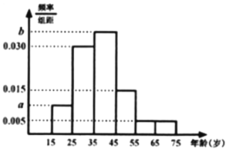
(1)求图中![]() 的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值
的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值![]() ;
;
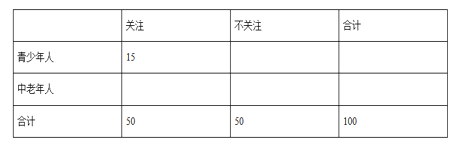
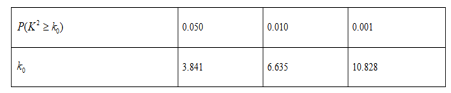
(2)若“青少年人”中有15人关注此活动,根据已知条件完成题中的![]() 列联表,根据此统计结果,问能否有
列联表,根据此统计结果,问能否有![]() 的把握认为“中老年人”比“青少年人”更加关注此活动?
的把握认为“中老年人”比“青少年人”更加关注此活动?
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据气象部门预报,在距离某个码头A南偏东45°方向的600km处的热带风暴中心B正以30km/h的速度向正北方向移动,距离风暴中心450km以内的地区都将受到影响,从现在起经过___小时后该码头A将受到热带风暴的影响(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ,
,![]() ,
,![]() 也成等比数列.
也成等比数列.
B.命题“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题是真命题.
”的逆命题是真命题.
C.“![]() 为真命题”是“
为真命题”是“![]() 为真命题”的充分不必要条件.
为真命题”的充分不必要条件.
D.命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,
,![]() ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学文化的优秀遗产,数学家刘徽在注解《九章算术》时,发现当圆内接正多边行的边数无限增加时,多边形的面积可无限逼近圆的面积,为此他创立了割圆术,利用割圆术,刘徽得到了圆周率精确到小数点后四位3.1416,后人称3.14为徽率,如图是利用刘徽的割圆术设计的程序框图,若结束程序时,则输出的![]() 为( )(
为( )(![]() ,
,![]() ,
,![]() )
)

A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过
经过![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,且与圆
有且仅有一个公共点,且与圆![]() 相交于
相交于![]() 两点,试问直线
两点,试问直线![]() 与
与![]() 的斜率之积
的斜率之积![]() 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学德育处为了解全校学生的上网情况,在全校随机抽取了40名学生(其中男、女生人数各占一半)进行问卷调查,并进行了统计,按男、女分为两组,再将每组学生的月上网次数分为5组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
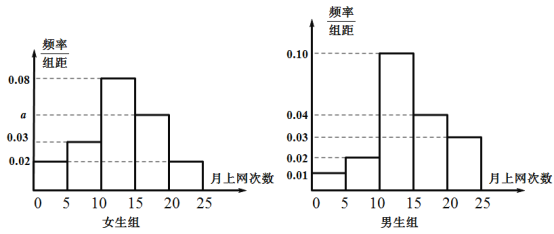
(1)写出女生组频率分布直方图中![]() 的值;
的值;
(2)求抽取的40名学生中月上网次数不少于15的学生人数;
(3)在抽取的40名学生中从月上网次数不少于20的学生中随机抽取3人,并用![]() 表示随机抽取的3人中男生的人数,求
表示随机抽取的3人中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型中华传统文化电视节目《![]() 中国诗词大会》以“赏中华诗词,寻文化基因,品生活之美”为宗旨,深受广大观众喜爱,各基层单位也通过各种形式积极组织、选拔和推荐参赛选手.某单位制定规则如下:(1)凡报名参赛的诗词爱好者必须先后通过笔试和面试,方可获得入围
中国诗词大会》以“赏中华诗词,寻文化基因,品生活之美”为宗旨,深受广大观众喜爱,各基层单位也通过各种形式积极组织、选拔和推荐参赛选手.某单位制定规则如下:(1)凡报名参赛的诗词爱好者必须先后通过笔试和面试,方可获得入围![]() 正赛的推荐资格;(2)笔试成绩不低于85分的选手进入面试,面试成绩最高的3人获得推荐资格.在该单位最近组织的一次选拔活动中,随机抽取了一个笔试成绩的样本,据此绘制成频率分布直方图(如图
正赛的推荐资格;(2)笔试成绩不低于85分的选手进入面试,面试成绩最高的3人获得推荐资格.在该单位最近组织的一次选拔活动中,随机抽取了一个笔试成绩的样本,据此绘制成频率分布直方图(如图![]() .同时,也绘制了所有面试成绩的茎叶图(如图2,单位:分).
.同时,也绘制了所有面试成绩的茎叶图(如图2,单位:分).

(Ⅰ)估计该单位本次报名参赛的诗词爱好者的总人数;
(Ⅱ)若从面试成绩高于(不含)中位数的选手中随机选取3人,设其中获得推荐资格的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com