½ā£ŗ£Ø1£©¢Ł

¢Śµ±a=1.1£¬x
0=2Ź±£¬f£Øx
0£©£¼0³ÉĮ¢
£Ø2£©ÉčĒśĻß

ÉĻĮ½øö¶Ō³ĘµćĪŖ£Øm£¬n£©£¬£Øn£¬m£©£¬
ÓŚŹĒ


ĖłŅŌp£¼0£»
£Ø3£©Ģį³öµÄĪŹĢāŹĒ£ŗµ±a”Ź£Ø0£¬e
-e£©Ź±£¬ŗÆŹży=a
xÓėy=log
axµÄĶ¼ĻóÓŠ3øö½»µć£»µ±a”Ź[e
-e£¬1£©Ź±£¬ŗÆŹży=a
xÓėy=log
axµÄĶ¼ĻóÓŠ1øö½»µć£®
ĪŹĢā½ā¾öČēĻĀ£ŗĻŌČ»£¬µ±0£¼a£¼1Ź±£¬ŗÆŹży=a
xÓėy=log
axµÄĶ¼ĻóŌŚÖ±Ļßy=xÉĻÓŠŅ»øö½»µć£®
ČōĒśĻßy=a
xÉĻÓŠĮ½øöµć£Øm£¬n£©£¬£Øn£¬m£©¹ŲÓŚÖ±Ļßy=x¶Ō³Ę£¬Ōņ

?

?

?mnlna=nlnn=mlnm£¬
¼“m£¬nŹĒŗÆŹży=xlnx£Ø0£¼x£¼1£©ÓėÖ±Ļßy=c£ØcĪŖ³£Źż£©µÄ½»µćµÄŗį×ų±ź£®
ŅņĪŖŗÆŹżf£Øx£©=xlnxÓŠČēĻĀŠŌÖŹ£ŗŌŚĒų¼ä
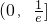
ÉĻµ„µ÷µŻ¼õ£¬ŌŚĒų¼ä
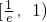
ÉĻµ„µ÷µŻŌö£®
ÓŚŹĒ

Ź±f£Øx£©=xlnxČ”µĆ×īŠ”Öµ
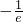
£¬¼“

£¬ÓÉĘäĶ¼ĻóæɵƵ½£¬µ±

Ź±£¬m£¬n³É¶Ō³öĻÖ£¬ĒŅ

£®”
µ±lna£¼-e£¬¼“a”Ź£Ø0£¬e
-e£©Ź±£¬µć£Øm£¬n£©£¬£Øn£¬m£©“ęŌŚ£¬¼“ŗÆŹży=a
xÓėy=log
axµÄĶ¼ĻóÓŠ3øö½»µć£»
µ±lna”Ż-e£¬¼“a”Ź[e
-e£¬1£©Ź±£¬µć£Øm£¬n£©£¬£Øn£¬m£©²»“ęŌŚ£¬ŗÆŹży=a
xÓėy=log
axµÄĶ¼ĻóÖ»ÓŠ1øö½»µć£®
·ÖĪö£ŗ£Ø1£©¢Łøł¾Żf£Ø3£©£¼0£¬a£¾1¹¹Ōģ²»µČŹ½×飬½ā²»µČŹ½×飬æɵĆaµÄȔֵ·¶Ī§£»
¢ŚÓÉ¢ŁÖŠ½įĀŪ£¬æɵĆaČ”£Ø1£¬1.445£©ÖŠµÄČĪŅāÖµ¶¼æÉŅŌ£¬½ų¶ųøų³öŗĻŹŹµÄx
0£¬¼“æɵƵ½“š°ø£®
£Ø2£©ÉčĒśĻß

ÉĻĮ½øö¶Ō³ĘµćĪŖ£Øm£¬n£©£¬£Øn£¬m£©£¬æɵĆp=-2m
2£¬½ų¶ųµĆµ½ŹµŹżpµÄȔֵ·¶Ī§£»
£Ø3£©Ģį³öµÄĪŹĢāŹĒ£ŗµ±a”Ź£Ø0£¬e
-e£©Ź±£¬ŗÆŹży=a
xÓėy=log
axµÄĶ¼ĻóÓŠ3øö½»µć£»µ±a”Ź[e
-e£¬1£©Ź±£¬ŗÆŹży=a
xÓėy=log
axµÄĶ¼ĻóÓŠ1øö½»µć£¬½ų¶ųøł¾Ż£Ø1£©£Ø2£©µÄ½įĀŪæɽųŠŠĶʵ¼ĀŪÖ¤£®
µćĘĄ£ŗ±¾Ģāæ¼²éµÄÖŖŹ¶µćŹĒÖøŹżŗÆŹżµÄĶ¼ĻóŗĶŠŌÖŹ£¬¶ŌŹżŗÆŹżµÄĶ¼ĻóŗĶŠŌÖŹ£¬·“ŗÆŹż£¬¾ßÓŠĻąµ±µÄÖ÷¹ŪŠŌ£¬ÄѶČŅ²±Č½Ļ“ó£®

 £Øp”Ł0£©ÉĻ“ęŌŚĮ½øö²»Ķ¬µć¹ŲÓŚÖ±Ļßy=x¶Ō³Ę£¬Ē󏵏żpµÄȔֵ·¶Ī§£»
£Øp”Ł0£©ÉĻ“ęŌŚĮ½øö²»Ķ¬µć¹ŲÓŚÖ±Ļßy=x¶Ō³Ę£¬Ē󏵏żpµÄȔֵ·¶Ī§£»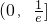 ÉĻµ„µ÷µŻ¼õ£¬ŌŚĒų¼ä
ÉĻµ„µ÷µŻ¼õ£¬ŌŚĒų¼ä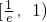 ÉĻµ„µ÷µŻŌö£®½āĢā¹ż³ĢÖŠæÉŅŌĄūÓĆ£»¢Ś½«øł¾ŻĢį³öŗĶ½ā¾öĪŹĢāµÄ²»Ķ¬²ć“ĪĒų±šøų·Ö£®£©
ÉĻµ„µ÷µŻŌö£®½āĢā¹ż³ĢÖŠæÉŅŌĄūÓĆ£»¢Ś½«øł¾ŻĢį³öŗĶ½ā¾öĪŹĢāµÄ²»Ķ¬²ć“ĪĒų±šøų·Ö£®£©
 ÉĻĮ½øö¶Ō³ĘµćĪŖ£Øm£¬n£©£¬£Øn£¬m£©£¬
ÉĻĮ½øö¶Ō³ĘµćĪŖ£Øm£¬n£©£¬£Øn£¬m£©£¬

 ?
? ?
? ?mnlna=nlnn=mlnm£¬
?mnlna=nlnn=mlnm£¬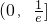 ÉĻµ„µ÷µŻ¼õ£¬ŌŚĒų¼ä
ÉĻµ„µ÷µŻ¼õ£¬ŌŚĒų¼ä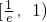 ÉĻµ„µ÷µŻŌö£®
ÉĻµ„µ÷µŻŌö£® Ź±f£Øx£©=xlnxČ”µĆ×īŠ”Öµ
Ź±f£Øx£©=xlnxČ”µĆ×īŠ”Öµ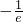 £¬¼“
£¬¼“ £¬ÓÉĘäĶ¼ĻóæɵƵ½£¬µ±
£¬ÓÉĘäĶ¼ĻóæɵƵ½£¬µ± Ź±£¬m£¬n³É¶Ō³öĻÖ£¬ĒŅ
Ź±£¬m£¬n³É¶Ō³öĻÖ£¬ĒŅ £®”
£®” ÉĻĮ½øö¶Ō³ĘµćĪŖ£Øm£¬n£©£¬£Øn£¬m£©£¬æɵĆp=-2m2£¬½ų¶ųµĆµ½ŹµŹżpµÄȔֵ·¶Ī§£»
ÉĻĮ½øö¶Ō³ĘµćĪŖ£Øm£¬n£©£¬£Øn£¬m£©£¬æɵĆp=-2m2£¬½ų¶ųµĆµ½ŹµŹżpµÄȔֵ·¶Ī§£»

