
 为正方形,
为正方形,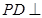 平面
平面 ,
,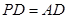 ,则
,则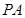 与
与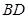 所成角的度数为
所成角的度数为
A.30° B.45° C.60° D.90°
C
【解析】
试题分析:以D为坐标原点,DA所在直线为x轴,DC所在线为y轴,DP所在线为z轴,建立空间坐标系,∵点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,令PD=AD=1
∴A(1,0,0),P(0,0,1),B(1,1,0),D(0,0,0)
 =(1,0,-1),
=(1,0,-1), =(-1,-1,0)
=(-1,-1,0)
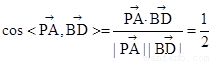 故两向量夹角的余弦值为
故两向量夹角的余弦值为  ,即两直线PA与BD所成角的度数为60°.故答案为:60°,选C.
,即两直线PA与BD所成角的度数为60°.故答案为:60°,选C.
考点:本题主要考查了异面直线所角的求法,由于本题中所给的背景建立空间坐标系方便,故采取了向量法求两直线所成角的度数,从解题过程可以看出,此法的优点是不用作辅助线,大大降低了思维难度
点评:解决该试题的关键是宜用向量法来做,以D为坐标原点,建立空间坐标系,求出两直线的方向向量,利用数量积公式求夹角即可.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届湖北省仙桃市高二下学期期中考试理科数学试卷(解析版) 题型:选择题
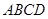 为正方形,
为正方形,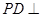 平面
平面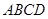 ,
,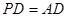 ,则
,则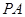 与
与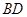 所成角的度数为
所成角的度数为
A.30° B.45° C.60° D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com