
����Ŀ����ͼ������S��ABCD�У�����ABCDΪֱ�����Σ�AB��CD��BC��CD��ƽ��SCD��ƽ��ABCD��SC=SD=CD=AD=2AB��M��N�ֱ�ΪSA��SB���е㣬EΪCD�е㣬��M��N��ƽ��MNPQ�ֱ���BC��AD���ڵ�P��Q���� ![]() =t
=t ![]() ��
�� 
��1����t= ![]() ʱ����֤��ƽ��SAE��ƽ��MNPQ��
ʱ����֤��ƽ��SAE��ƽ��MNPQ��
��2���Ƿ����ʵ��t��ʹ�ö����M��PQ��A��ƽ��ǵ�����ֵΪ ![]() �������ڣ����ʵ��t��ֵ���������ڣ�˵�����ɣ�
�������ڣ����ʵ��t��ֵ���������ڣ�˵�����ɣ�
���𰸡�
��1��֤����EΪCD�е㣬���ı���ABCEΪ���Σ�
��AE��CD��
��t= ![]() ʱ��QΪAD�е㣬PQ��CD������PQ��AE��
ʱ��QΪAD�е㣬PQ��CD������PQ��AE��
��ƽ��SCD��ƽ��ABCD��SE��CD����SE����ABCD��
��PQ��ABCD����PQ��SE����PQ����SAE��
������MNPQ����SAE
��2���⣺��ͼ����EΪԭ�㣬ED��EA��ESֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ����ͼ��ʾ����ϵ��
��ED=a����M����1��t��a���� ![]() ��
�� ![]() ��a��
��a�� ![]() a����E��0��0��0����A��0��
a����E��0��0��0����A��0�� ![]() ��0����
��0����
Q����1��t��a�� ![]() ��0����
��0���� ![]() =��0��
=��0�� ![]() ��
�� ![]() ����
����
��ABCDһ����������Ϊ ![]() =��1��0��0����
=��1��0��0����
��ƽ��MPQ�ķ����� ![]() =��x��y��z����
=��x��y��z����
��  ��ȡz=2����
��ȡz=2���� ![]() =��0��
=��0�� ![]() ��2����
��2����
ƽ��ABCD�ķ�����Ϊ ![]() =��0��0��1��
=��0��0��1��
�߶����M��PQ��A��ƽ��ǵ�����ֵΪ ![]() ��
��
�������⣺cos��= ![]() =
= 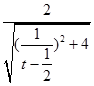 =
= ![]() ��
��
���t= ![]() ��t=
��t= ![]() ��
��
��ͼ��֪����t= ![]() ʱ�������M��PQ��AΪ�۶���ǣ��������⣬��ȥ
ʱ�������M��PQ��AΪ�۶���ǣ��������⣬��ȥ
���ϣ�t= ![]() ��
��

����������1���Ƶ���AE��CD��PQ��AE���Ӷ�SE����ABCD���ɴ���֤����MNPQ����SAE����2����EΪԭ�㣬ED��EA��ESֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ���ռ�ֱ������ϵ�����������������t��ֵ��
�����㾫�������ڱ��⿼���ƽ����ƽ�洹ֱ���ж�����Ҫ�˽�һ��ƽ�����һ��ƽ��Ĵ��ߣ���������ƽ�洹ֱ���ܵó���ȷ�𰸣�


 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ķ�����ΪR��f����2��=2021��������x�ʣ����ޣ�+�ޣ�������f'��x����2x��������ʽf��x����x2+2017�Ľ⼯Ϊ�� ��
A.����2��+�ޣ�
B.����2��2��
C.�����ޣ���2��
D.�����ޣ�+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ������ϵxOy�У�����C1�� ![]() ����Ϊ������������ƽ��ֱ������ϵ��ԭ��OΪ���㣬x���������Ϊ���ᣬȡ��ͬ��λ���ȵļ�����ϵ�У�����C2����sin��
����Ϊ������������ƽ��ֱ������ϵ��ԭ��OΪ���㣬x���������Ϊ���ᣬȡ��ͬ��λ���ȵļ�����ϵ�У�����C2����sin�� ![]() ��=1��
��=1��
��1��������C1����ͨ���̺�����C2��ֱ�����귽�̣�
��2������C1��ǡ�ô���������ͬ�ĵ㵽����C2�ľ�����ȣ��ֱ�����������ļ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������E��![]() �Ľ���ΪF������F��ֱ��l��E����A��C����
�Ľ���ΪF������F��ֱ��l��E����A��C����
��1���ֱ��A��C������������E�����ߣ���֤��������E��A��C���㴦�������ഹֱ��
��2������F��ֱ��l�Ĵ�����������E����B��D���㣬���ı���ABCD���������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪F1��F2�ֱ���˫���� ![]() ��
�� ![]() =1��a��0��b��0�������ҽ��㣬����F2��˫���ߵ�һ��������ƽ�е�ֱ�߽�˫������һ���������ڵ�M������M�����߶�F1F2Ϊֱ����Բ�⣬��˫���������ʵ�ȡֵ��Χ�ǣ� ��
=1��a��0��b��0�������ҽ��㣬����F2��˫���ߵ�һ��������ƽ�е�ֱ�߽�˫������һ���������ڵ�M������M�����߶�F1F2Ϊֱ����Բ�⣬��˫���������ʵ�ȡֵ��Χ�ǣ� ��
A.��1�� ![]() ��
��
B.�� ![]() ��+�ޣ�
��+�ޣ�
C.�� ![]() ��2��
��2��
D.��2��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽��ο������ı仯���ɣ�������η����������ռ���������2014��1����2016��12���ڼ��½Ӵ��ο�������λ�����ˣ������ݣ����������������ͼ�� 
���ݸ�����ͼ�����н��۴�����ǣ� ��
A.�½Ӵ��ο�����������
B.��Ӵ��ο�����������
C.������½Ӵ��ο����߷��ڴ�����7��8��
D.����1����6�µ��½Ӵ��ο��������7����12�£������Ը�С���仯�Ƚ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�������������ͼ��ͼ��ʾ.

��1����˼�����ı������
��2�������![]() ������ͼ����ʾλ�ã�
������ͼ����ʾλ�ã�![]() Ϊ�����߶��е㣬
Ϊ�����߶��е㣬![]() Ϊ���㣬���ڼ���������ϣ���
Ϊ���㣬���ڼ���������ϣ���![]() �㵽
�㵽![]() ������·���ij�.
������·���ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xex��a��x��1����a��R��
��1��������f��x����x=0���м�ֵ����a��ֵ��f��x���ĵ�������
��2��������ʵ��x0�ʣ�0�� ![]() ����ʹ��f��x0����0����ʵ��a��ȡֵ��Χ��
����ʹ��f��x0����0����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ  ��tΪ����������������ԭ��OΪ���㣬x���������Ϊ����ļ�����ϵ�У�����C�ļ����귽��Ϊ��=2
��tΪ����������������ԭ��OΪ���㣬x���������Ϊ����ļ�����ϵ�У�����C�ļ����귽��Ϊ��=2 ![]() cos��
cos�� ![]() +�ȣ���
+�ȣ���
��I����ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
������ֱ��l������C�ཻ��M��N���㣬��|MN|��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com