
分析 联立已知直线方程解方程组可得入射点,在入射线再取一点可得求关于l2的对称点,可得l的方程.
解答 解:联立$\left\{\begin{array}{l}{x-y+1=0}\\{2x+y-4=0}\end{array}\right.$可解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,即入射点为A(1,2),
在直线l1上再取一点P(0,1),则P关于l2的对称点为P′(m,n),
则$\left\{\begin{array}{l}{\frac{n-1}{m}(-2)=-1}\\{2•\frac{m}{2}+\frac{n+1}{2}-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{12}{5}}\\{n=\frac{11}{5}}\end{array}\right.$,即P′($\frac{12}{5}$,$\frac{11}{5}$),
由反射的知识可知反射光线所在的直线l即为AP′,
可得其斜率k=$\frac{2-\frac{11}{5}}{1-\frac{12}{5}}$=$\frac{1}{7}$,故直线方程为y-2=$\frac{1}{7}$(x-1),
整理为一般式可得x-7y+13=0
故答案为:x-7y+13=0
点评 本题考查直线的对称关系,涉及方程组的解法和直线的点斜式方程,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -10 | B. | -9 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
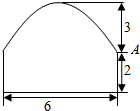 一条隧道横截面由一段抛物线及矩形的三边围成,各段长度见图中所示(单位:米),某卡车空载时可通过此隧道.
一条隧道横截面由一段抛物线及矩形的三边围成,各段长度见图中所示(单位:米),某卡车空载时可通过此隧道.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com