
���� ��1������֪�������õȲ����е�ͨ�ʽ��ǰn���ʽ�г������飬����������ɴ����������{an}��ǰn��ͣ�
��2����nΪż��ʱ����n=2k��k��N*�����T2k=2k����������ˣ�2����nΪ����ʱ����n=2k-1��k��N*�����T2k-1=1-2k����������ˣ�-4���ɴ�������˵�ȡֵ��Χ��
��3���������������m��n��n��m��2����ʹ��S2��Sm-S2��Sn-Sm�ɵȱ����У��ɴ�������֪�����Ƶ�����ʽ��2n-m2+2����2n+m2-2��=12���������Ӷ��õ�������������m��n��n��m��2����ʹ��S2��Sm-S2��Sn-Sm�ɵȱ����У�
��� �⣺��1��������{an}�Ĺ���Ϊd��
��2a5-a3=13��S4=16��
��$\left\{\begin{array}{l}2��a1+4d��-��a1+2d��=13\\ 4a1+6d=16\end{array}$�����a1=1��d=2������2�֣�
��an=2n-1��Sn=n2������4�֣�
��2���ٵ�nΪż��ʱ����n=2k��k��N*��
��T2k=��a2-a1��+��a4-a3��+��+��a2k-a2k-1��=2k�� ����5�֣�
���벻��ʽ��Tn��[an+1+��-1��n+1an]•2n-1���æ�•2k��4k���Ӷ��ˣ�$\frac{4k}{2k}$��
��f��k��=$\frac{4k}{2k}$����f��k+1��-f��k��=$\frac{4k+1}{2��k+1��}$-$\frac{4k}{2k}$=$\frac{4k��3k-1��}{2k��k+1��}$��
��k��N*����f��k+1��-f��k����0����f��k���ǵ����ģ���f��k��min=2��
��ˣ�2������7�֣�
�ڵ�nΪ����ʱ����n=2k-1��k��N*��
��T2k-1=T2k-��-1��2ka2k=2k-��4k-1��=1-2k������8�֣�
���벻��ʽ��Tn��[an+1+��-1��n+1an]•2n-1���æ�•��1-2k������2k-1��4k��
�Ӷ��ˣ�-4k��
��k��N*����-4k�����ֵΪ-4�����Ԧˣ�-4��
���ϣ��˵�ȡֵ��ΧΪ-4���ˣ�2������10�֣�
��3���������������m��n��n��m��2����ʹ��S2��Sm-S2��Sn-Sm�ɵȱ����У�
��Sm-S2��2=S2•��Sn-Sm��������m2-4��2=4��n2-m2����
��4n2=��m2-2��2+12����4n2-��m2-2��2=12������12�֣�
����2n-m2+2����2n+m2-2��=12������14�֣�
��n��m��2����n��4��m��3����2n+m2-2��15��
��2n-m2+2�����������ʽ��2n-m2+2����2n+m2-2��=12��������
�ʲ�����������m��n��n��m��2����ʹ��S2��Sm-S2��Sn-Sm�ɵȱ����У� ����16�֣�
���� ���⿼�����е�ǰn��͵�������ʵ����ȡֵ��Χ�������������������������Ƿ���ڵ��жϣ��ۺ���ǿ���Ѷȴ���ʱҪע�ⲻ��ʽ�����������ԡ���֤���ĺ������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | O | B�� | $\frac{3}{2}$ | C�� | 2 | D�� | -l |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
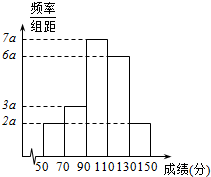 ������ij��ѧ��ʦ�������̵�2015�������X�����������Y����ѧ���ĸ߿���ѧ�ɼ��У������ȡ20��ѧ���ijɼ����Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
������ij��ѧ��ʦ�������̵�2015�������X�����������Y����ѧ���ĸ߿���ѧ�ɼ��У������ȡ20��ѧ���ijɼ����Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45 | B�� | 65 | C�� | 80 | D�� | 130 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com