练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知△ABC三内角A、B、C所对边的长分别为a，b，c，且3sin2A+3sin2B＝4sinAsinB+3sin2C．

    （1）求cosC的值；

    （2）若a＝3，c，求△ABC的面积．

    【答案】（1）；（2）或．

    【解析】

    （1）利用正弦定理对已知代数式化简，根据余弦定理求解余弦值；

    （2）根据余弦定理求出b＝1或b＝3，结合面积公式求解.

    （1）已知等式3sin2A+3sin2B＝4sinAsinB+3sin2C，利用正弦定理化简得：3a2+3b2﹣3c2＝4ab，即a2+b2﹣c2ab，

    ∴cosC；

    （2）把a＝3，c，代入3a2+3b2﹣3c2＝4ab得：b＝1或b＝3，

    ∵cosC，C为三角形内角，

    ∴sinC，

    ∴S△ABCabsinC3×bb，

    则△ABC的面积为或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知多面体ABCDEF中，四边形ABFE为正方形，，，G为AB的中点，.

    （1）求证：平面CDEF；

    （2）求平面ACD与平面BCF所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

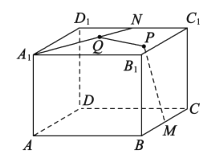
    【题目】已知长方体中，底面ABCD的长AB=4，宽BC=4，高=3，点M，N分别是BC，的中点，点P在上底面中，点Q在上，若，则PQ长度的最小值是

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x-85.71，则下列结论中不正确的是

    A. y与x具有正的线性相关关系

    B. 回归直线过样本点的中心（，）

    C. 若该大学某女生身高增加1cm，则其体重约增加0.85kg

    D. 若该大学某女生身高为170cm，则可断定其体重比为58.79kg

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知符号函数sgnx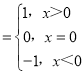f（x）是定义在R上的减函数，g（x）＝f（x）﹣f（ax）（a＞1），则（ ）

    A.sgn[g（x）]＝sgn xB.sgn[g（x）]＝﹣sgnx

    C.sgn[g（x）]＝sgn[f（x）]D.sgn[g（x）]＝﹣sgn[f（x）]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）＝etx（t＞0），过点P（t，0）且平行于y轴的直线与曲线C：y＝f（x）的交点为Q，曲线C过点Q的切线交x轴于点R，若S（1，f（1）），则△PRS的面积的最小值是_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2＋ax＋b，g(x)＝ex(cx＋d)，若曲线y＝f(x)和曲线y＝g(x)都过点P(0，2)，且在点P处有相同的切线y＝4x＋2．

    (1)求a，b，c，d的值；

    (2)若x≥－2时，恒有f(x)≤kg(x)，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，是两个不重合的平面，在下列条件中，可判断平面，平行的是（ ）

    A.，是平面内两条直线，且，

    B.，是两条异面直线，，，且，

    C.面内不共线的三点到的距离相等

    D.面，都垂直于平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.（其中常数，是自然对数的底数.）

    （1）讨论函数的单调性；

    （2）证明：对任意的，当时，.

    查看答案和解析>>

    同步练习册答案