
分析 (I)$\frac{{S}_{n}}{n}$=an-n+1,Sn=nan-n(n-1),当n≥2时,Sn-1=(n-1)an-1-(n-1)(n-2),化为an-an-1=2,利用等差数列的通项公式即可得出.
(II)${b_n}={a_n}•{3^{a_n}}$=(2n-1)•32n-1=$\frac{1}{3}(2n-1)•{9}^{n}$,利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(I)∵$\frac{{S}_{n}}{n}$=an-n+1,∴Sn=nan-n(n-1),当n≥2时,Sn-1=(n-1)an-1-(n-1)(n-2),
两式相减可得:an=nan-(n-1)an-1-2(n-1),化为an-an-1=2,
∴数列{an}是等差数列,首项为1,公差为2.
∴an=1+2(n-1)=2n-1.
(II)${b_n}={a_n}•{3^{a_n}}$=(2n-1)•32n-1=$\frac{1}{3}(2n-1)•{9}^{n}$,
∴数列{bn}前n项的和Tn=$\frac{1}{3}[9+3×{9}^{2}$+5×93+…+(2n-1)•9n],
9Tn=$\frac{1}{3}[{9}^{2}+3×{9}^{3}$+…+(2n-3)•9n+(2n-1)•9n+1],
∴-8Tn=$\frac{1}{3}[9+2({9}^{2}+{9}^{3}+…+{9}^{n})-(2n-1)•{9}^{n+1}]$=$\frac{1}{3}[2×\frac{9×({9}^{n}-1)}{9-1}-9-(2n-1)•{9}^{n+1}]$=$\frac{5-8n}{12}×{9}^{n+1}-\frac{15}{4}$,
∴Tn=$\frac{8n-5}{96}×{9}^{n+1}$+$\frac{15}{32}$.
点评 本题考查了“错位相减法”与等比数列的前n项和公式、递推关系的应用,考查了推理能力与计算能力,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
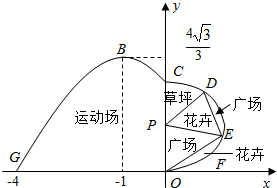 如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.
如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4030}{4031}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com