分析:(1)先求出导函数f'(x),设出切点(x
0,y
0),然后根据在x=x
0的导数等于切线的斜率,切点在切线和函数f(x)的图象上,建立方程组,解之即可求出b的值;
(2)①构造函数
h(x)=f(x)-x2-m=x3-x2-3x-m,利用导数研究函数h(x)的单调性,转化成使h(x)图象在(0,+∞)内与x轴有两个不同的交点,建立关系式,解之即可求出m的范围.②做差比较较x
1x
2+9与3(x
1+x
2)的大小.
解答:解:(1)∵
f(x)=x3-bx,∴f'(x)=x
2-b
设切点为(x
0,y
0),依题意得
解得:b=3
(2)设
h(x)=f(x)-x2-m=x3-x2-3x-m则h'(x)=x
2-2x-3=(x+1)(x-3).
1令h'(x)=023,得x=-14或x=35在(0,3)6上,h'(x)<07,
故h(x)在(0,3)上单调递减,在(3,+∞)上,h'(x)>0,
故h(x)在(3,+∞)上单调递增,
若使h(x)图象在(0,+∞)内与x轴有两个不同的交点,
则需
,∴-9<m<0
此时存在x>3时,h(x)>0,例如当x=5时,
h=-25=15-m=-m>0.
∴①所求m的范围是:-9<m<0.
②由①知,方程f(x)=x
2+m2在(0,+∞)3上有两个解x
1,x
2,
满足0<x
1<3,x
2>3,x
1x
2+9-3(x
1+x
2)=(3-x
1)(3-x
2)<0,
x
1x
2+9<3(x
1+x
2).
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数与方程的综合运用等基础题知识,考查运算求解能力、推理论证能力,考查化归与转化思想,属于中档题.



 一课一练课时达标系列答案
一课一练课时达标系列答案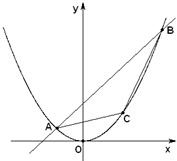 已知直线y=2x+k被抛物线x2=4y截得的弦长AB为20,O为坐标原点.
已知直线y=2x+k被抛物线x2=4y截得的弦长AB为20,O为坐标原点.