练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

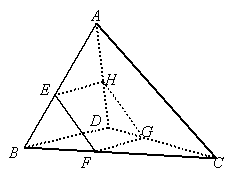
    如图所示，已知空间四边形ABCD，E、F分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且，求证直线EF、GH、AC交于一点．

    同解析。


    解析:

    如答图所示，∵AE＝EB，AH＝HD，∴EH//BD，且EH＝BD，

    ∵，∴FG//BD，且FG＝BD，

    ∴EH//FG，且EH≠FG，

    故四边形EFGH为梯形，则EF与GH必相交，

    设交点为P，P∈平面ABC，又P∈平面DAC，

    又平面BAC∩平面DAC＝AC，故P∈AC，

    即EF、GH、AC交于一点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    我们将底面是正方形，侧棱长都相等的棱锥称为正四棱锥．已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同，且如图所示，视图中四边形ABCD是边长为1的正方形，则该几何体的体积为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

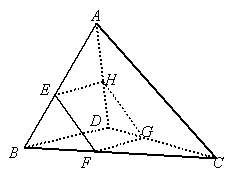
    如图所示，已知平面与空间四边形ABCD的四条边

    AB、BC、CD、DA分别交于E、F、G、H，

    若四边形EFGH是平行四边形.求证：BD//，AC//.

       

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    如图所示，已知平面与空间四边形ABCD的四条边

    AB、BC、CD、DA分别交于E、F、G、H，

    若四边形EFGH是平行四边形.求证：BD//，AC//.

       

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年上海市崇明县高三高考模拟考试二模理科数学试卷（解析版） 题型：解答题

    如图，已知四棱锥的底面ABCD为正方形，平面ABCD，E、F分别是BC，PC的中点，，．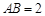

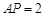    （1）求证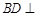：平面；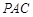

    （2）求二面角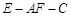的大小．

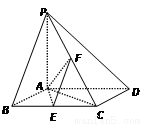
    【解析】第一问利用线面垂直的判定定理和建立空间直角坐标系得到法向量来表示二面角的。

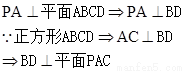
    第二问中，以A为原点，如图所示建立直角坐标系

    ，，

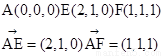    设平面FAE法向量为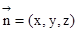，则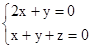

    ，，

     

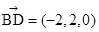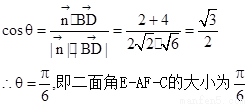
    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省福州三中高三（上）期中数学试卷（解析版） 题型：选择题

    我们将底面是正方形，侧棱长都相等的棱锥称为正四棱锥．已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同，且如图所示，视图中四边形ABCD是边长为1的正方形，则该几何体的体积为（ ）

    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案