
【题目】口袋中装有2个白球和n(n≥2,n![]() N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
(I)用含n的代数式表示1次摸球中奖的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;
(III)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)当f(p)取得最大值时,n的值为2.
;(III)当f(p)取得最大值时,n的值为2.
【解析】试题分析:
(1)由题意结合古典概型公式可得所求概率值为![]() ;
;
(2)利用二项分布可得3次摸球中恰有1次中奖的概率是![]() ;
;
(3)结合概率函数的解析式可得当f(p)取得最大值时,n的值为2.
试题解析:
(I)设“1次摸球中奖”为事件A,则P(A)=![]() ,
,
(II)由(I)得,若n=3,则1次摸球中奖的概率为p=![]() =
=![]() =
=![]() ,
,
所以3次摸球中,恰有1次中奖的概率为P3(1)=![]() ,
,
(III)设“1次摸球中奖”的概率为p,
则3次摸球中,恰有1次中奖的概率为
f(p)=C![]() p(1-p)2 =3p3-6p2+3p(0<p<1),
p(1-p)2 =3p3-6p2+3p(0<p<1),
因为f'(p)=9p2-12p+3=3(p-1)(3p-1),
所以,当p∈(0, ![]() )时,f(p)单调递增;当p∈(
)时,f(p)单调递增;当p∈(![]() ,1)时,f(p)单调递减,
,1)时,f(p)单调递减,
所以,当p=![]() 时,f(p)取得最大值.
时,f(p)取得最大值.
令![]() ,解得n=2,n=1(舍去).
,解得n=2,n=1(舍去).
所以,当f(p)取得最大值时,n的值为2.


科目:高中数学 来源: 题型:
【题目】某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
x | … | 30 | 40 | 45 | 50 | … |
y | … | 60 | 30 | 15 | 0 | … |
(1)在所给的坐标系中,如图,根据表格提供的数据描出实数对(x,y)的对应点,并确定y与x的一个函数关系式y=f(x);
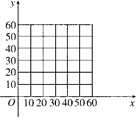
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市将建一个制药厂,但该厂投产后预计每天要排放大约80吨工业废气,这将造成极大的环境污染.为了保护环境,市政府决定支持该厂贷款引进废气处理设备来减少废气的排放,该设备可以将废气转化为某种化工产品和符合排放要求的气体,经测算,制药厂每天利用设备处理废气的综合成本![]() (元)与废气处理量
(元)与废气处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理
,且每处理![]() 吨工业废气可得价值为
吨工业废气可得价值为![]() 元的某种化工产品并将之利润全部用来补贴废气处理.
元的某种化工产品并将之利润全部用来补贴废气处理.
(1)若该制药厂每天废气处理量计划定位20吨时,那么工厂需要每天投入的废气处理资金为多少元?
(2)若该制药厂每天废气处理量计划定为![]() 吨,且工厂不用投入废气处理资金就能完成计划的处理量,求
吨,且工厂不用投入废气处理资金就能完成计划的处理量,求![]() 的取值范围;
的取值范围;
(3)若该制药厂每天废气处理量计划定为![]() (
(![]() )吨,且市政府决定为处理每吨废气至少补贴制药厂
)吨,且市政府决定为处理每吨废气至少补贴制药厂![]() 元以确保该厂完成计划的处理量总是不用投入废气处理资金,求
元以确保该厂完成计划的处理量总是不用投入废气处理资金,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
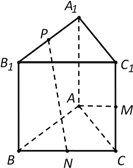
【题目】如图,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据市场分析,南雄市精细化工园某公司生产一种化工产品,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.写出月总成本y(万元)关于月产量x(吨)的函数关系.已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(
,(![]() ).
).
(1)若函数![]() 与
与![]() 的图象在
的图象在![]() 上有两个不同的交点,求实数
上有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(2)若在![]() 上不等式
上不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:对于![]() 时,任意
时,任意![]() ,不等式
,不等式![]() 恒成立.
恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com