
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,则________.(写出所有正确结论的编号)
,则________.(写出所有正确结论的编号)
①四面体![]() 每个面的面积相等
每个面的面积相等
②四面体![]() 每组对棱相互垂直
每组对棱相互垂直
③连接四面体![]() 每组对棱中点的线段相互垂直平分
每组对棱中点的线段相互垂直平分
④从四面体![]() 每个顶点出发的三条棱的长都可以作为一个三角形的三边长
每个顶点出发的三条棱的长都可以作为一个三角形的三边长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元. (Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮胎集团有限公司生产的轮胎的宽度![]() (单位:
(单位: ![]() )服从正态分布
)服从正态分布![]() ,公司规定:轮胎宽度不在
,公司规定:轮胎宽度不在![]() 内将被退回生产部重新生产.
内将被退回生产部重新生产.
(1)求此轮胎不被退回的概率(结果精确到![]() );
);
(2)现在该公司有一批轮胎需要进行初步质检,检验方案是从这批轮胎中任取![]() 件作检验,这
件作检验,这![]() 件产品中至少有
件产品中至少有![]() 件不被退回生产部,则称这批轮胎初步质检合格.
件不被退回生产部,则称这批轮胎初步质检合格.
()求这批轮胎初步质检合格的概率;
()若质检部连续质检了![]() 批轮胎,记
批轮胎,记![]() 为这
为这![]() 批轮胎中初步质检合格的批数,求
批轮胎中初步质检合格的批数,求![]() 的数学期望.
的数学期望.
附:若![]() ,则
,则![]()
![]()
![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() =(﹣
=(﹣ ![]() sinωx,cosωx),
sinωx,cosωx), ![]() =(cosωx,cosωx),ω>0,记函数f(x)=
=(cosωx,cosωx),ω>0,记函数f(x)= ![]()
![]() ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客的购物总额(单位元),将数据按照
位顾客的购物总额(单位元),将数据按照![]()
![]() ,
,![]()
![]() 分成
分成![]() 组,制成了如下图所示的频率分布直方图:
组,制成了如下图所示的频率分布直方图:
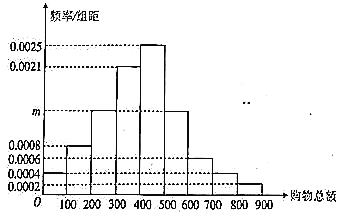
该商场每日大约有![]() 名顾客,为了增加商场销售总额,近期对一次性购物不低于
名顾客,为了增加商场销售总额,近期对一次性购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(1)求频率分布直方图中![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(2)若每日按分层抽样的方法从购物总额在![]() 三组对应的顾客中抽取
三组对应的顾客中抽取![]() 名顾客,这
名顾客,这![]() 名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线![]() ,
,![]() ,和圆:
,和圆:![]() 相切,则实数
相切,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() 或
或![]() B.
B. ![]() 或
或![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com